geometria analityczna
Matijaz: Okrąg o: x2+y2−6√2 x+10=0 jest opisany na sześciokącie ABCDEF.
a) wyznacz współrzędne wierzchołków sześciokąta wiedząc że odcięta jest równa √2
b) oblicz pole figury F=F1−F2 gdzie F1 jest sześciokątem zaś F2 kołem wpisanym w ten
sześciokąt
6 sty 17:12
Matijaz: Doszedłem do tego, że S (3√2,0), r= 2√2 i A(√2, 0)
6 sty 17:15
Tadeusz:
x
2−6
√2x+18+y
2−18+10=0
(x−3
√2)
2+y
2=8
dalej sam −

6 sty 17:18
Tadeusz:
dla x=√2 otrzymasz chyba dwa punkty
6 sty 17:19
Matijaz: To juz mam

6 sty 17:20
Matijaz: Chyba jeden

6 sty 17:21
Tadeusz:
... przepraszam .... jeden
6 sty 17:23
Matijaz: Ok

a jak mam policzyć pozostałe punkty?
6 sty 17:25
Tadeusz:
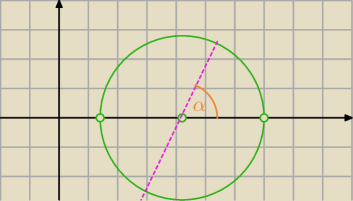
a jakiż to kąt i ile to tgα ...itd
6 sty 17:28
Matijaz: Nie rozumiem

6 sty 17:44
Tadeusz:
a jak powstaje sześciokąt foremny ... na jakie części dzielimy kąt 360
o
tg60
=
?
Napiszesz równanie prostej przez środek okręgu o znanym współczynniku kierunkowym
i poszukasz punktów przecięcia się z okręgiem
Drugi sposób:
wiesz, że bok sześciokąta to promień okręgu
6 sty 17:51
Matijaz: Proszę o pomoc

6 sty 17:52
Tadeusz:
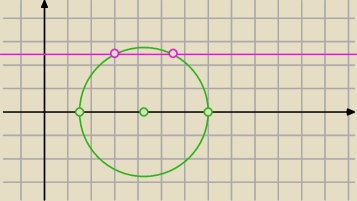
6 sty 17:54
Matijaz: Dzięki wielkie

6 sty 17:54
Tadeusz:
−

6 sty 17:55
Tadeusz:
"zaskoczył"

?−

6 sty 17:56
Matijaz: Tak

6 sty 18:17
Tadeusz: −

6 sty 18:43



 a jak mam policzyć pozostałe punkty?
a jak mam policzyć pozostałe punkty?
 a jakiż to kąt i ile to tgα ...itd
a jakiż to kąt i ile to tgα ...itd

 ?
Napiszesz równanie prostej przez środek okręgu o znanym współczynniku kierunkowym
i poszukasz punktów przecięcia się z okręgiem
Drugi sposób:
wiesz, że bok sześciokąta to promień okręgu
?
Napiszesz równanie prostej przez środek okręgu o znanym współczynniku kierunkowym
i poszukasz punktów przecięcia się z okręgiem
Drugi sposób:
wiesz, że bok sześciokąta to promień okręgu




 ?−
?−

