Całka podstawienie cz2 bezendu: ∫e^x√1+e^xdx t=1+e^x dt=e^xdx

	2
∫√tdt=∫t1/2dt=		t3/2+C
	3

	2
=		(ex+1)3/2+C
	3

?

Eve: oki

bezendu: A tutaj jakie podstawienie ∫(2x+1)⁷dx t=2x+1 ?

Eve: tak, tylko dobrze oblicz dx

Dawid: t=2x+1 dt=2dx

dt
	=dx
2

1		1		1
	∫t7dt=		*		t8
2		2		8

Eve:

bezendu: Nie koniecznie chciałem, żebyś za mnie rozwiązywał....

Dawid: Przepraszam

bezendu: Oblicz podaną całkę przybliżając ją za pomocą sumy prostokątów: ∫¹₀ xdx

Eve: tu ci nie pomogę, nie pamiętam, sorki

bezendu: :(

Eve: nie wiem czy o to chodzi ale tu coś znalazłam http://www.algorytm.org/procedury-numeryczne/calkowanie-numeryczne-metoda-prostokatow.html

Eve: tam trzeba mieć z jaka dokładnością

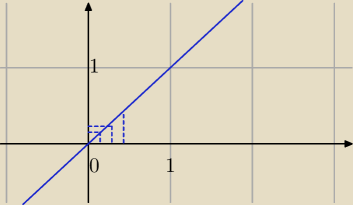
Mila: Dzielimy odcinek<0,1> na 10 jednakowych części. Ustalamy długość przedziałów;

1
10

	1
szerokość prostokąta :
	10

	1		2		10
wysokość odpowiednio :		,		,...
	10		10		10

Sumujemy pola prostokątów

1		1		1		2		1		3		1		10
	*		+		*		+		*		+..........+		*		=
10		10		10		10		10		10		10		10

	1		1		2		3
=		*(		+		+		................+1)
	10		10		10		10

	1		110+1
S≈		*		*10=0,55
	10		2

Teraz uogólnij na n przedziałów i oblicz granicę.

bezendu:

	ex
∫
	1+e2x

t=1+e^2x dt=2e^2xdx hmm co dalej ?

Eve: e^2x=(e^x)² więc chyba lepiej e^x=t

niechciany: https://www.youtube.com/watch?v=ZEoSSnsGiT0 − 4:30

bezendu: Dziękuję.