proszę o rozwiązanie Michał: W pojemniku jest n kul białych i k kul czrnych Z pojemnika losujemy dwie kule . Prawdopodobieństwo wylosowania dwóch kul różnych kolorów jest równe prawdopodobieństwu wylosowania dwóch kul tego samego koloru . Wykaż że (n − k)² = n + k czyli P ({bc , cb}) = P ( { bb, cc}) n² − 2nk + k² −n − k =0 nie wiem jak to wykazać

Maslanek: Korzystając z informacji w zadaniu poszukaj zależności n od k.

Michał: czyli n² +n(2k − 1) = k − k² n² +n(2k − 1) − k + k² = 0 Δ = 4k² − 4k + 1 − 4( − k + k²) = 4k² − 4k + 1 +4k − 4k² = 1 k₁ = −k lub k₂ = −k+2 nie wiem czy dobrze

Mila: Masz obliczyć prawdopodobieństwa w zależności od n i k.

	n+k 2
|Ω|=

A − wylosowano dwie kule tego samego koloru B− wylosowano dwie kule różnych kolorów

	n 2   k 2   +
P(A)=
	n+k 2

P(A)=P(B)⇔

n 2   k 2   +		n*k
	=		⇔
n+k 2		n+k 2

1		1
	n*(n−1)+		k*(k−1)=n*k⇔
2		2

n*(n−1)+k*(k−1)=2n*k⇔ n²−n+k²−k−2nk=0 n²−2nk+k²=n+k⇔ (n−k)²=n+k cnw

Michał: dziękuję bardzo moje rozumowanie było zupełnie nieprawidłowe

Mila: Tak, źle myślałeś.

Michał: mam jeszcze zadanie

	1		1		3
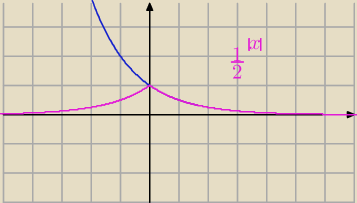
Rozwiąż graficznie równanie (		)IxI − 1 = −		x2 + 2x− 2
	2		2		4

	1
zrobiłem tak narysowałem wykres funkcji g(x) = (		)IxI i wykres funkcji
	2

	1		7		1
f(x) = −		x2 + 2x −		xw = 1 yw = −
	2		4		2

i wykresy te nie mają wspólnych punktów a wynik wynosi x = 2 współrzędna ta spełnia oba równania

Mila:

	1
y=(		)|x|
	2

Mila:

	−1		7
y=		x2+2x−
	2		4

	−2
xw=		=2
	2*−12

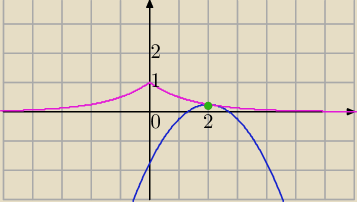
	−1		7		7		1
f(2)=		*4+4−		=2−		=		=yw
	2		4		4		4

spr.

1		1
	2=
2		4

Michał: dziękuję MIli rzeczywiście żle obliczyłem wierzchołek

Michał: mam jeszcze jedno zadanie Trójkąt równoramienny o obwodzie p obraca się wokół podstawy Jakie wymiary powinien mieć trójkąt, aby powstała w ten sposób bryła miała możliwie największą objętość . wyznacz tę objętość wiem że powstają dwa stożki i że trzeba wyrazić objętość bryły joko funkcję długości podstawy trójkąta b − ramiona trójkąta a − podstwa

	1		3
wyniki to a =		p −długość podstawy b =		p − długość ramion
	4		8

znowu robię pewnie jakieś błędy bo nic mi nie wychodzi

Michał:

	π
wynik Vmax =		p3
	96

Mila: AB=a a+2b=p 2b=p−a

	p−a
b=
	2

	1
R2=b2−		a2
	4

	(p−a)2		1		p2−2ap+a2−a2
R2=		−		a2=
	4		4		4

	1
Vf=2Vs=2*		*πR2*h
	3

	1		p2−2ap		1
Vf=		*2*π*		*		a
	3		4		2

	π*(p2*a−2a2p		πp
Vf(a)=		=		*(ap−2a2)
	12		12

	−p		p
aw=		=
	−2*2		4

	πp		p		p2		πp3
Vf=		*(		*p−2*		)=
	12		4		16		96

Michał: mój błąd polegał na tym że a = CC^,i dlatego nie mogłem wybrnąć dziękuję bardzo

Mila: