Dowod geometrycznych
Kinga: W czworokącie ABCD przekątne są prostopadłe oraz na tym czworokącie można opisać okrąg o środku
w punkcie O. udowodnij, że łamana Abc dzieli czworokat ABCD na dwie figury o równych polach.
6 sty 15:31
Tadeusz:
... to odpowiedz sobie na pytanie cóż to za czworokąt ...
6 sty 15:39
5-latek: Witaj.
czy ja dobrze mysle ze to bedzie albo romb albo kwadrat ?
6 sty 15:41
Tadeusz:
a na każdym rombie opiszesz kwadrat ....czy tylko na szczególnym? −
A może są inne czworokąty ?
6 sty 15:49
Kinga: Ja to narysowalam ze jest to deltoid i jedna przekątna leży na średnicy okregu to wtedy jest
łatwo udowodnić ale nie jestem pewna czy ja to Dobrze rozrysowuje.
6 sty 15:53
Tadeusz:
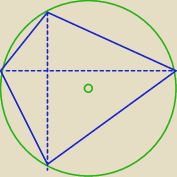
... a swoją drogą zadanie jest zapisane nieprecyzyjnie
Teza słuszna tylko jeśli punkt 0 jest punktem przecięcia się przekątnych a zarazem środkiem
okręgu opisanego
6 sty 15:58
Tadeusz:
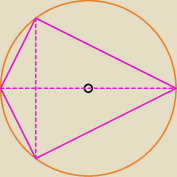
... masz rację .. O nie musi być punktem przecięcia się przekątnych
ale musi leżeć na średnicy
6 sty 16:03
Kinga: Musi? W tym przypadku co narysowales Wyżej nie Leży a też wydaje się być zgodne z zadaniem
6 sty 16:08
Tadeusz:
... to co narysowałem wyżej pokazuje, że pola równe nie są
6 sty 16:21
Kinga: Czyli tylko ten drugi przypadek jest właściwy. Dzięki
6 sty 16:28
Mila:
W treści zadania czegoś brakuje, albo tw. nieprawdziwe.
6 sty 16:35
Mila:
Łamana chyba powinna być zamknięta?
6 sty 16:36
Tadeusz:
łamana wyznacza punkty na obwodzie ... ale to teą tak "swoimi" słowami
Brak uściślenia punktu 0
6 sty 18:06