liczby zespolone modułi argument monika: Mam pytanie (liczby zespolone rozumiem) ale to zadanie inaczej było zrobione na ćwiczeniach a inaczej ja je robię Wyznacz moduł i argument i narysuj liczbę zespoloną. −3−3i. Ja to rozwiązuje tak |z|=√(−3)²+(−3i)²=0 bo jeżeli −3i ² to wychodzi 9 a że i² jest −1 to −9. Na zajęciach zrobiliśmy tak √9+9=√18 Czy ma być √18?

asdf: liczba zespolona to po prostu dwie liczby uporzadkowane w taki sposob: pierwsza nazwana "rzeczywista", druga "urojona". z = a + bi; real(z) = a; imaginary(z) = b; jesli czesc zespolona = 0, mozna ja zapisac jako: z = a + 0bi = a modul liczby rzeczywistej to |a|, modul liczby urojonej to tez |z|, w taki sposob: |z| = √a² + b², żadne i!

asdf: poszukaj interpretacje geometryczna (modul sie liczy z tw. pitagorasa...)

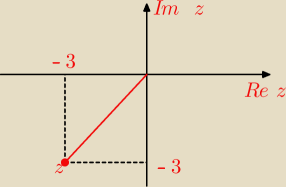
Janek191: z = − 3 − 3 i I z I = √ (−3)² + ( − 3)² = √9 + 9 = √9*2 = 3√2

	− 3		1		√2
cos φ =		= −		= −
	3√2		√2		2

	− 3		√2
sin φ =		= −
	3 √2		2

więc argument liczby z

	π		5
φ = 180o + 45o = π +		=		π
	4		4