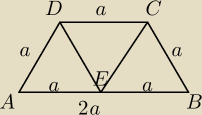
Trapez i trójkąty równoboczne xcc: W trapezie ABCD dane są: |AB|=2a, |BC|=|CD|=|DA|=a. Oblicz długości odcinków, na jakie dzieli przekątne trapezu punkt przecięcia się tych przekątnych. Mój problem jest taki, że wiem jak zrobić to zadanie, żeby wyszedł dobrze wynik − te 3 trójkąty są w domyśle równoboczne i ich wysokości zawierają się w przekątnych − ale nie wiem jak udowodnić, że rzeczywiście są one równoboczne, a dokładniej jak wykazać, że |DE|=|EC|=a?

===: ... a jaka jest miara kąta DAB ?

xcc: Domyślam się, że 60, ale jak do tego dojść?

Metis: ale jak do tego dojść? Trójkąt równoboczny

xcc: Ok, już wiem, z cosinusa wystarczy wyliczyć, bo przekątna BD pada na DA pod kątem prostym − to łatwo udowodnić. Takie proste, a nie zauważyłem. Dzięki za małą podpowiedź

===: ...zabłądziłeś ... czy o drogę pytasz? −

===: −

xcc: Metis, ja muszę dojść do tego, że jest to tr. równoboczny, więc nie mogę skorzystać z jego własności, ale już napisałem wyżej jak to zrobić, chyba o to chodziło?

Metis: Nie czytałem zadania

xcc: Choć w sumie powiedziałem, że łatwo udowodnić, że BD jest prostopadłe do DA, to znów mam problem jak to wykazać . Gdyby EC było prostopadłe do AD to, nie byłoby problemu z tym, bo wysokość byłaby prostopadła do obu tych odcinków, ale jak znów teraz udowodnić, że EC jest prostopadłe do AD? (pewnie okaże się, że banalne i wyjdę na głupka )

===: ... chyba już zasypiasz −

xcc: Ani mi nie mów, cały dzień robiłem zadania i zrobiłem wszystko oprócz tego i już nie wytrzymuje powoli . Jeśli wiesz jak, to zlituj się nad biednym człowiekiem

===: DB dzieli kąt EDC na?

xcc: Połowy, czyli zmierzasz do tego, że trójkąt BED jest równoramienny i tyle trzeba było?

===: narysuj te przekątne ....a zobaczysz wszystko Pytałeś o kąt ADB .... jeśli do ADE dołożę 30^o to ... ? −

xcc: Hmm, ale koniec końców my jeszcze teoretycznie nie wiemy ile kąt ADE ma, bo ja cały czas próbuję udowodnić ile ma kąt DAB, żeby wykazać, że jest to trójkąt równoboczny, a żeby to udowodnić, to muszę wykazać, że ADB jest prosty. Wiem, że trochę chaotyczne to co napisałem, ale chyba tak właśnie jest . Ale znalazłem inny sposób dzięki tej przekątnej. Trójkąty DBE i DBC są przystające c(kbk), czyli DE jest równy a i to koniec moich problemów z tym zadaniem, ale możesz rozwinąć swój sposób, bo być może czegoś nadal nie rozumiem (a to całkiem prawdopodobne

xcc: O boże, teraz przeczytałem co napisałem wcześniej ze zrozumieniem i niezłą gafę popełniłem, tam miało być EC RÓWNOLEGŁE do AD i być może dlatego się nie zrozumieliśmy , ale nadal mimo rozwiązania zadania tym sposobem z przystawaniem, nie wiem jak udowodnić tę równoległość tych odcinków.

===: ... zostaw to na jutro ... bo już nie kontaktujesz − Czego nie wiesz ... że kąt ADE ma 60^o ? Skoro EAD ma 60 a na przeciwko równych boków leżą równe kąty ... a boki są a i a ...to chyba oczywista oczywistość −

Metis: A skąd pewność że ∡EAD ma 60 skoro nie wiemy czy jest to trójkąt równoboczny czy nie

xcc: "Hmm, ale koniec końców my jeszcze teoretycznie nie wiemy ile kąt ADE ma, bo ja cały czas próbuję udowodnić ile ma kąt DAB(...)" (DAB, lub jak napisałeś EAD). Sorry, że jestem upierdliwy, ale na prawdę jeszcze nie udowodniliśmy, że EAD ma 60 stopni, jeśli masz czas i chęci to przeczytaj wszystkie posty i tam napisałem, że żeby to udowodnić z tego cosinusa, który wyszedłby 1/2, to musimy pierwsze udowodnić, że trójkąt ADB jest prostokątny, a to udowodnimy jeżeli odcinki AD i EC będą równoległe. No chyba, że coś pominąłem i już gdzieś zostało udowodnione, że EAD to 60 stopni, a może masz jakiś inny sposób niż tym cosinusem? Jeszcze raz przepraszam za problemy, ale chciałbym być pewny w tym zadaniu, bo to jedyne, którego nie umiałem

===: ... to już pytanie poniżej granicy śmiechu −

===: patrz mój post z 22:33

xcc: "Skoro EAD ma 60(...)" I tak w kółko , ale skąd wiemy, że kąt EAD ma 60?

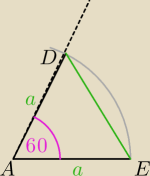
===: ∡ADE=∡AED bo oba leżą na przeciwko równych boków TO MUSZĄ MIEĆ PO 60^o !

===: (180−60):2

xcc: Naprawdę chyba muszę być baardzo zmęczony, bo nadal nie rozumiem. Owszem, zgodzę się, że ∡ADE=∡AED, bo to tr. równoramienny (|AE|=|AD|), ale skąd się tam wzięło, że kąt EAD jest równy 60 stopni?, cały czas rozchodzi mi się o ten kąt.

Eta:

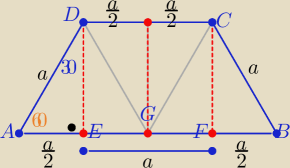
|AE|		1
	=		=sin30o , to |∡BAD|=60o
|AD|		2

i td.................................

Metis: A ja z tym kątem 60⁰ to nadal bym się sprzeczał

xcc: Eta już wytłumaczyła jak go udowodnić, w sumie banał, hahah , dziękuję Ci. Tobie ===: również za cierpliwość i próbę wytłumaczenia. Pozdrawiam serdecznie

Eta:

Metis: