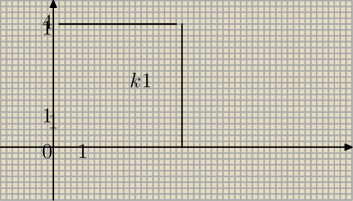
 a) Kwadrat K2 jest obrazem kwadratu K1(rysunek) w symetrii względem prostej y=x+2. Oblicz pole
części wspólnej K1∩K2. Proszę wytłumaczcie mi to dokładnie krok po kroku bo robie to którys
raz i mi nie wyszło
a) Kwadrat K2 jest obrazem kwadratu K1(rysunek) w symetrii względem prostej y=x+2. Oblicz pole
części wspólnej K1∩K2. Proszę wytłumaczcie mi to dokładnie krok po kroku bo robie to którys
raz i mi nie wyszło 

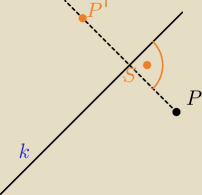 Narysuj sobie na kartce układ współrzędnych, kwadrat, prostą y=x+2.
Zegnij kartkę wzdłuż tej prostej i szpilką nakłuj wierzchołki, otrzymasz obrazy punktów A, B,
C, D.
Masz przykład punktów symetrycznych względem prostej k.
PP'⊥k
|SP|=|SP'|
Przeciez w gimnazjum rysowałeś odbicia symetryczne.
Narysuj sobie na kartce układ współrzędnych, kwadrat, prostą y=x+2.
Zegnij kartkę wzdłuż tej prostej i szpilką nakłuj wierzchołki, otrzymasz obrazy punktów A, B,
C, D.
Masz przykład punktów symetrycznych względem prostej k.
PP'⊥k
|SP|=|SP'|
Przeciez w gimnazjum rysowałeś odbicia symetryczne.
 a skąd mam wiedziec ze toamto jest prostopadłe fo k
Punkt przecięcia prostych P1 : −x=x+2
x=−1, y=1
P1(−1,1) jest środkiem AA'
xa+0
−1=
2
1=U{ya+0}⇔
A'(xa,ya)=(−2,2)
Możesz tak wyznaczyć wsp. pozostałych punktów B',C' D'. i tego nie rozumiem vco ja tutaj mam
zrobić
a skąd mam wiedziec ze toamto jest prostopadłe fo k
Punkt przecięcia prostych P1 : −x=x+2
x=−1, y=1
P1(−1,1) jest środkiem AA'
xa+0
−1=
2
1=U{ya+0}⇔
A'(xa,ya)=(−2,2)
Możesz tak wyznaczyć wsp. pozostałych punktów B',C' D'. i tego nie rozumiem vco ja tutaj mam
zrobić
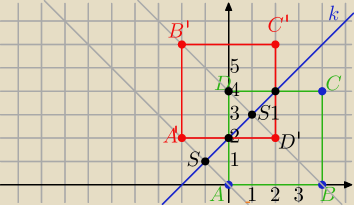 Prowadzimy prostopadłe do k przechodzące przez A,B,C,D.
k: y=x+2
prostopadłe do k maja równania:
y=−x+b, b ustalimy dla każdego z punktów
a: y=−x Prosta przechodzi przez punkt (0,0) więc b=0
Punkt przecięcia prostych:
y=−x i y=x+2⇔
x+2=−x⇔x=−1 i y=−(−1)=1 ,S=(−1,1) jest to środek odcinka AA'
Prowadzimy prostopadłe do k przechodzące przez A,B,C,D.
k: y=x+2
prostopadłe do k maja równania:
y=−x+b, b ustalimy dla każdego z punktów
a: y=−x Prosta przechodzi przez punkt (0,0) więc b=0
Punkt przecięcia prostych:
y=−x i y=x+2⇔
x+2=−x⇔x=−1 i y=−(−1)=1 ,S=(−1,1) jest to środek odcinka AA'
| xA+xA' | yA+yA' | |||
xs= | i ys= | postawiamy wspórzędne | ||
| 2 | 2 |
| 0+xA' | 0+yA' | |||
−1= | i 1= | ⇔ | ||
| 2 | 2 |
| 4+xB' | 0+yB' | |||
1= | i 3= | ⇔B'=(−2,6) | ||
| 2 | 2 |
| 0+xD' | 4+yB' | |||
1= | i 3= | ⇔D'=(2,2) | ||
| 2 | 2 |