czy dobrze proszę o sprawdzenie Michał:

	x−6
Dana jest funkcja f(x) =		Wykaż że styczne do wykresu funkcji f poprowadzone w
	x−3

punktach przecięcia wykresu funkcji z osiami układu współrzędnych są równoległe

	x−6
f(x) =		= x + b l : y = ax + b i ma z f(x) jeden punkt wspólny
	x−3

	x−6		x+3 −9		9
f(x) =		=		= 1 −
	x−3		x + 3		x+3

x−6
	= x + b ⇒ x − b = x2 + bx + 3x + 3b ⇒ x2 + ( b+ 2) x + 3b +6 = 0
x−3

Δ= 0 Δ = b² + 4b +4 − 4 ( 3b + 6 ) = 0 ⇒ b² − 8b − 20 = 0 Δ₁ =144 √144 =12 b₁ = −2 b₂ = 10 czyli są dwie proste k: y = x − 2 i l : y = x +10 ⇒ k II l

Mila: Dlaczego zmieniłeś mianownik z (x−3) na (x+3). Ponadto, czy masz na lekcjach pochodne?

===: ... matematyka to nie rysunki −

Michał: tam w mianowniku ma być x−3 a pochodne miałem i zastanawiałem jak to zrobić również też jest błąd przy porównaniu a mianowicie powinno być

x − 6
	= x +b ⇒ x − 6 =( x − 3 )( x +b) = x2 −3x +bx − 3b⇒ x2 − (3−b) *x −4b
x − 3

Δ = b² +10b +9 =0 Δ₁ = 64 √64 = 8 czyli b₁ = −1 b₂ = −9 czyli proste to y = x −1 i y = x − 9 przepraszam wkradł się błąd jeżeli chodzi o pochodną to f^,(x) = U{(x−3)−(x −6)}{(x − 3 )² = 0 jakoś mi to zapisanie nie wychdzi

===: ... jak coś błędnie założysz ... to brniesz już w to ...

	x−6
Powiedz mi skąd wytrzasnąłeś to		=x+b
	x−3

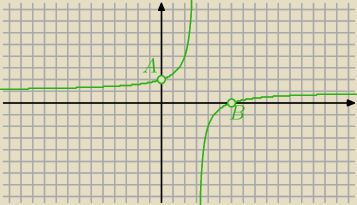
===: A=(0, 2) B=(6, 0)

	x−3−x+6		3
f'(x)=		=
	(x−3)2		(x−3)2

f'(0)=1/3 f'(6)=3/9=1/3 O równania stycznych nie pytają .. a współczynniki kierunkowe mają równe −

Michał: bo prosta i f(x) mają mieć wspólny punkt styczności ale teraz pomyślałem że chyba trzeba rzeczywiście zrobić to pochodną i tak

	3
f,(x) =		= 0 x ≠ 3
	(x−3)2

i skorzystać z ze wzoru y − f(x₀) = f^,(x₀) ( x − x₀) ale nie wiem jakie będzi mieć współrzędne punkt styczności

Michał: zanim ja coś napiszę to === już napisał ale w treści pisze że styczne mają być równoległe

Michał: ale jak obliczyłeś współrzędne A= (0 ,2 ) i b = ( 6 ,0)

===:

	x−6
1. Zapis		=x+b jest błędny
	x−3

Zakładasz bowiem, że współczynnik kierunkowy jest 1

	x−6
Gdybyś jeszcze napisał		=ax+b ...ale to nie ta "ścieżka"
	x−3

2. Punkty styczności określone są w treści zadania 3. Nie pytają Cię o równania stycznych 4. Pochodna w punkcie oznacza tangens kąta nachulenia stycznej czyli współczynnik kierunkowy 5. Proste mające takie same współczynniki kierunkowe są równoległe

===: Twoje pytanie z 22:43 jest poniżej granicy śmiechu −

Michał: to już zrozumiałem ale nadal nie wiem jak obliczyłeś współrzędne A i B

Michał: nie wiem czy dobrze myślę f(0) = 2 ⇒ A = (0,2)

	(x−6)
a		= 0 ⇒ x=0 czyli B =(6,0)
	(x−3)

===: Człowieku ... nie umiesz wyznaczyć współrzędnych punktów przecięcia się wykresu funkcji z osiami ? −

===: a jednak −

Michał: przepraszam ale chyba jest póżno i dlatego zrobiłem wielką gafę jeszecze raz dziękuję za dyskusję jeżeli chodzi o odpowiedż 22;43 to rzeczywiście założylem że a = 1 czyli tg = 45⁰

Mila:

	x−6
f(x)=
	x−3

D =R\{3} Punkt przecięcia z OY:

	−6
x=0 to f(0)=		=2 ⇔A=(0,2)
	−3

Punkt przecięcia z osią OX , to obliczamy miejsce zerowe f(x)

x−6
	=0⇔x−6=0⇔
x−3

x=6 B=(6,0)

Mila: 2) styczne : y=f'(x₀)*x+b

	1*(x−3)−(x−6)*1
f'(x)=		⇔
	(x−3)2

	3
f'(x)=
	(x−3)2

Styczna w p. A(0,2)

	3		3		1
f'(0)=		=		=
	(0−3)2		9		3

	1
y=		x+b
	3

styczna w p. B=(6,0)

	3		1
f'(6)=		=
	(6−3)2		3

	1
y=		x+b'
	3

Styczne mają jednakowe wsp. kierunkowe zatem są prostymi równoległymi.

===: −

Mila: dla ===

Michał: dziękuję MILI za uwagi

Mila: To rozwiązania.

Michał: słusznie za rozwiązania jeszcze raz dziękuję Mili