Jakie wymiary musi mieć stożek, aby jego objętość była jak największa? nikk: Przekrój osiowy stożka jest trójkątem o obwodzie 24. Jakie wymiary musi mieć ten stożek, aby jego objętość była jak największa?

Eve:

	24−a
a+2b=24⇒b=
	2

	1
V=		πr2H
	3

H²=b²−r² a=2r wyraź V za pomocą r i oblicz pochodną, która przyrównaj do 0

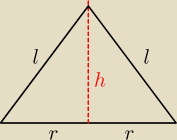
Janek191: 2 r + 2 l = 24 / : 2 r + l = 12 ⇒ l = 12 − r h² + r² = l² = ( 12 − r)² h² + r² = 144 − 24 r + r² h² = 144 − 24 r ; r ∊ ( 0 ; 6 ) h = √ 144 − 24 r więc objętość

	1		π
V =		π r2*h =		r2*√ 144 − 24 r
	3		3

Pytanie: były pochodne ?

nikk: Były

Janek191: To fajnie Oblicz ekstremum − maksimum funkcji V(r)