całki obliczanie pól figur mat: Pole figury ograniczonej krzywymi: y=x³ i y=x⁵ można to zapisać jako:

	x4		x6		1		1
2∫(od 0 do 1) (x3 − x5) dx = 2(		−		)|(od 0 do 1) = 2*		=
	4		6		12		6

bo te dwie figury wyjda takie same, nie? bo w odpowiedziach własnie podają tak jakby wynik jeden figury czyli jest 2 razy mniejszy od tego wyniku który mi wychodzi

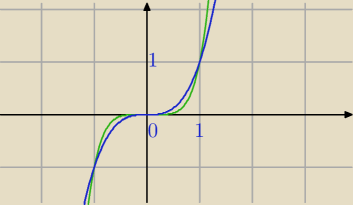Mila: f(x)=x³ g(x)=x⁵ x³=x⁵⇔ x⁵−x³=0 x³(x²−1)=0 x=0 punkt przecięcia (0,0) x=1 punkt przecięcia (1,1) x=−1 punkt przecięcia (−1,−1) Masz dwa obszary symetryczne względem punktu (0,0)

	1		1
P=2*0∫1(x3−x5) dx=2*[		x4−		x6]01=
	4		6

	1		1		3		2		1		1
=2*[		−		]=2*(		−		)=2*		=
	4		6		12		12		12		6