Dla jakich wartości parametru m Sandra: Hey. Mam pytanko jak rozwiązać poniższe zadanie? Dla jakich wartości parametru m zbiorem rozwiązania nierówności

x2 − mx −2
	> −1
x2 − 3x + 4

jest zbiór wszystkich liczb rzeczywistych?

AROB: Pomagam

AROB: Zał. x² − 3x + 4 = 0 ⇒ Δ < 0 ⇒ brak miejsc zerowych ⇒ D = R

x2 − mx − 2
	+ 1 > 0
x2 − 3x + 4

x2 − mx − 2 + x2 − 3x + 4
	> 0
x2 − 3x +4

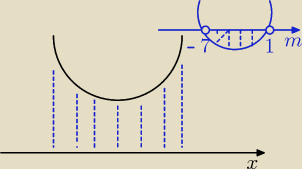
(2x² + x(−m−3) + 2) (x² − 3x + 4) > 0 I I I brak miejsc zerowych Na podst. wykresu: Δ < 0 ⇔ b² − 4ac < 0 a=2, b= −m−3, c=2 (−m−3)² − 4*2*2 < 0 m² + 6m + 9 − 16 < 0 m² + 6m − 7 < 0 ⇒ Δ₁ = 64, √Δ₁ = 8, m₁ = 1, m₂ = −7 Na podst.wykresu (niebieski) : Odp. m ∊ (−7, 1)