Optymalizacja-największe pole trójkąta prostokątnego cakelock: Rozważmy trójkąty prostokątne, których przeciwprostokątne mają 10cm. Znajdź długość przyprostokątnych trójkąta, który ma największe pole. Oblicz je.

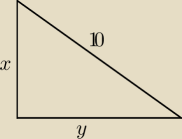
Marshall: x² + y² = 10 y = √100−x², po wyznaczeniu dziedziny x∊<−10,10>, ale intuicyjnie ograniczamy dziedzinę do x∊(0,10), jako że mowa o długości oraz, zależy nam na tym, aby jednak ten trójkąt istniał, dlatego wykluczamy 10 z dziedziny. Czyli Pole (P) możemy uzależnić od zmiennej x. P(x) = 0,5x √100−x² = √25x² − 0,25x⁴.

dP		1
	(lub po prostu pochodna P'(x) ) =		* 50x − x3
dx		2 √25x2 − 0,25x4

Wyznaczając dziedzinę otrzymujemy przedział x∊(−∞,−10) suma (0,10), odrzucamy pierwszą część, jako że mówimy o długości i otrzymujemy przedział, który wyszedł wcześniej. Szukamy ekstremów, przyrównując pochodną do 0. P(x) = 0 ⇔ 50x − x³ = 0 ⇔ x∊{ − √50. 0, √50 } Jedynie x = √50 należy do dziedziny, w tymże punkcie też pochodna zmienia swój znak z plusa na minus, a więc x ten daje maksimum lokalne dla funkcji oznaczającej pole. P = 0,5 * √50 * √50 = 25 To moje pierwsze zadanie rozwiązane na tej stronie na poważnie, mam nadzieję, że wszystko w porządku i że będę gościć tu cześciej.

pigor: .., niech x,a=?== − szukane długości przyprostokątnych, to P(x)=¹₂xa i a=√10²−x² i x²<10² ⇒ ⇒ P(x)= ¹₂x√100−x² i 0< x<10 , no to pobaw się w znalezienie ekstremum lokalnego (max) tej funkcji pola P. ...