geometria analityczna Kinia: W trójkąt rownoboczny ABC o wierzcholku C=(3,−5) wpisano okrąg o środku S=(−1,−3). Wyznacz współrzędne wierzchołków A i B. Obliczylam wysokość trójkąta, długość boku trójkąta, zauważyłam, ze A i B będą należeć do okręgu o środku S i promieniu 2/3 h . Napisałam równanie tegoż okręgu i nie mam pomysłu co dalej ...

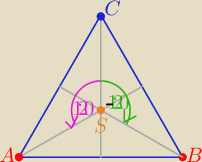
Eta: Z obrotu punktu C wokół punktu S o 120^o otrzymujemy punkt A Z obrotu punktu C wokół punktu S o −120^o otrzymujemy punkt B Dawniej w szkole średniej były równania obrotu : x^'= (x_C−x_S)*cosα−(y_C−y_S)*sinα+x_S y^'=(x_C−x_S)*sinα+(y_C−y_S)*cosα+y_S i takie zadanie było łatwizną cos120^o= cos(−120^o)= −0,5 , sin120^o= 0,5√3 , sin(−120^o)= −0,5√3 po podstawieniu otrzymujemy: A( −3+√3;−2+2√3) , B( −3−√3;−2−2√3) i bingo

Eta: 2 sposób 1/ równanie okręgu opisanego na tym trójkącie 2/ wyznaczenie środka D podstawy AB 3/ wyznaczenie równania prostej AB⊥CD 4/ rozwiązanie układu tych równań okręgu i prostej AB daje odp A(....,...) B(....,...) Dobranoc Wszystkim nocnym Markom

Eta: Odpowiedź można sprawdzić

xA+xB+xC		yA+yB+yC
	= xS ⋀		= yS
3		3