z trapezu wycieto koło, powstałą figurę obrócono dookoła prostej.
ninaxx:
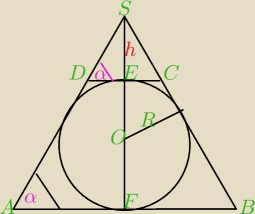
Mógłby ktoś podpowiedzieć co dalej?
Z trapezu równoramiennego o dłuższej podstawie a i kącie ostrym α, w który można wpisać okrąg
wycięto koło wpisane w ten trapez. Powstałą figurę obrócono dookoła prostej przechodzącej
przez środek koła i środki podstaw trapezu. Oblicz objętość powstałej bryły.
H−wysokość dużego stożka
h− wysokość małego stożka
r− promień podstawy małego stożka
12a − promień podstawy dużego stożka
H=
12atgα
h= rtgα
V=
13 π [
a24H−r
2h−4R
3]
i pytanko co z tym dalej zrobić

4 sty 21:52
Gray: Widzę trójkąt, myślę
Mila 
4 sty 21:52
bezendu:
Eta ?
4 sty 21:54
Mila:
Tak , ale trójkąty tylko na geometrii.

4 sty 22:09
Gray:
"Nie wybrnę z tego z twarzą..."
Grey.
4 sty 22:10
ninaxx: Czyli nie jest mi nikt w stanie pomóc?
4 sty 22:10
Mila:
Oj, pomogę, poczekaj chwilę.
4 sty 22:15
4 sty 23:15
ninaxx: Przepraszam ale czy wΔCMB tgα nie powinien wyglądać tak: tgα=
hse 
4 sty 23:15
Mila:
Tak, miał być ctgα, przepraszam, dobrze, że czytasz i analizujesz.
4 sty 23:21
Mila:
Jutro przepiszę bez błędu, dziś już nie. A masz odpowiedź?
4 sty 23:22
ninaxx: niestety nie
4 sty 23:25
Mila:
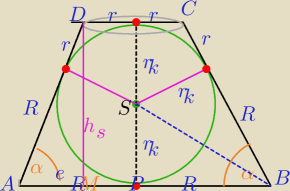
|AB|=a
h
s− wysokość stożka ściętego
r
k− promień koła (promień kuli wpisanej w stożek ścięty) wpisanego w trapez
WΔSPB:
================
=================
w ΔAMD:
e=h
s*ctgα
2r=a−2e
| | α | |
2r=a*(1−2tg |
| *ctgα)−średnica górnej podstawy stożka ściętego |
| | 2 | |
| | 1 | | α | | a2 | | a2 | | α | | α | |
Vs= |
| π*a*tg |
| *[ |
| + |
| *(1−2tg |
| *ctgα)+a2*(1−2tg |
| *ctgα)2] |
| | 3 | | 2 | | 4 | | 4 | | 2 | | 2 | |
Doprowadź do prostszej postaci.
| | 4π | | 1 | | α | |
Vfigury=Vs− |
| *( |
| a* tg |
| )3 |
| | 3 | | 2 | | 2 | |
4 sty 23:55
Mila: ?
5 sty 00:01
Gray: Dzięki
Mila 
5 sty 00:31
Eta:
Bardzo dziękuję
Mila 

5 sty 00:35
ninaxx: Mam jeszcze pewną wątpliwość w objętości stożka ścietego bo skoro srednica górnej podstawy
wynosi a (1−2tg α2 ctgα) to promień to 12 a (1−2tg α2 ctgα) a jakby nie bylo
podniosła Pani do kwadratu średnicę, czyż nie?
5 sty 11:36
Mila:
Posprawdzaj i podnieś wartość promienia, to przecież oczywiste.
5 sty 15:54
 Mógłby ktoś podpowiedzieć co dalej?
Z trapezu równoramiennego o dłuższej podstawie a i kącie ostrym α, w który można wpisać okrąg
wycięto koło wpisane w ten trapez. Powstałą figurę obrócono dookoła prostej przechodzącej
przez środek koła i środki podstaw trapezu. Oblicz objętość powstałej bryły.
H−wysokość dużego stożka
h− wysokość małego stożka
r− promień podstawy małego stożka
12a − promień podstawy dużego stożka
H=12atgα
h= rtgα
V=13 π [a24H−r2h−4R3]
i pytanko co z tym dalej zrobić
Mógłby ktoś podpowiedzieć co dalej?
Z trapezu równoramiennego o dłuższej podstawie a i kącie ostrym α, w który można wpisać okrąg
wycięto koło wpisane w ten trapez. Powstałą figurę obrócono dookoła prostej przechodzącej
przez środek koła i środki podstaw trapezu. Oblicz objętość powstałej bryły.
H−wysokość dużego stożka
h− wysokość małego stożka
r− promień podstawy małego stożka
12a − promień podstawy dużego stożka
H=12atgα
h= rtgα
V=13 π [a24H−r2h−4R3]
i pytanko co z tym dalej zrobić



 |AB|=a
|AB|=a


