narysuj wykres f-cji Akatsuki: Narysuj wykres funkcji y=x+sinx gdzie 0<=x<=2pi Proszę o pomoc w narysowaniu za pomocą tabelki. Potrzebne mi jest to do zadania, ale nie potrafię narysować tego wykresu

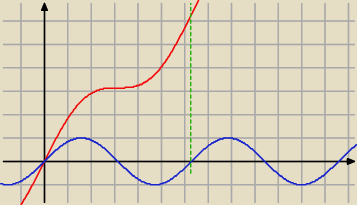
PW: Tak prymitywnie, na zasadzie dodawania wartości w "węzłowych" punktach i domyślania się jak wykres wygląda między nimi? Narysuj wykres funkcji f(f) = x na przedziale [0,2π]. Pod spodem wykres funkcji g(x) = sinx na tym samym przedziale. Dla x = 0 obie mają wartość 0, a więc h(x) = f(x) + g(x) = 0+0 = 0.

	π
Na przedziale [0,		] obie funkcje są rosnące, a więc ich suma też jest funkcją rosnącą.
	2

Liczymy:

	π
h(		) = f({π}{2}) + g({π}{2}) = {π}{2} + 1.
	2

Mamy więc jakieś wyobrażenie: − na przedziale [0,{π}{2}] funkcja h jest rosnąca, w lewym krańcu osiąga wartość 0, w prawym − wartość {π}{2} + 1. Już to można jakoś w przybliżeniu narysować.

	3π
Podobnie myśląc o dwóch funkcjach rosnących narysujemy wykres h na przedziale [		, 2π].
	2

Na pozostałych przedziałach nie jest tak łatwo (funkcja f rośnie, funkcja g maleje) − pomyśl sam.

===: