romb Eta: Dla Mateusza Oblicz pole rombu o boku 17 cm, w którym długości przekątnych różnią się o 14 cm Podobnym sposobem, jak w zadaniach z liczbami, które Ci z Milą podałyśmy

Eta: Ojj widzę,że Mateusz poszedł już lulu

Arcyksiążę: Tak.

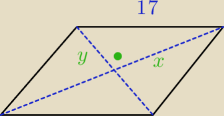
Arcyksiążę: x,y∊R₊ d₁−dłuższa przekątna x−y=7⇒x=7+y d₂−krótsza przekątna d₁−d₂=17

	d1*d2
P=
	2

a=17 x−połowa dłuższej przekątnej y−połowa krótszej przekątnej x²+y²=17² (7+y)²+y²=17² 49+14y+y²+y²=289 2y²+14y−240=0 / :2 y²+7y−120=0 (y+3,5)²−132,25=0 (y+3,5)²−(11,5)²=0 (y+3,5−11,5)(y+3,5+11,5)=0 (y−8)(y+15)=0 y=8 lub y=−15 x=7+8=15cm P=120cm²

Arcyksiążę: d₁−d₂=14 Tam drobna pomyłka

Eta: e, f −− długości przekątnych a −− długość boku a=17 i f−e=14

	e*f
f2+e2=4a2= 4*289 ⇒ (f−e)2+2ef=4*289 ⇒ 196+2ef=4*289 /:4 ⇒		=289−49
	2

ef
	=P =240 cm2
2