funkcje liniowe i wartość bezwzględna
bartosz: | | x + 3 | |
Określ dziedzinę i miejsce zerowe funkcji y = |
| |
| | |x+3| − 5 | |
3 sty 20:22
Metis: Dziedzina |x+3| − 5≠0
Miejsca zerowe:
x+3=0...
3 sty 20:24
bartosz: Mógłbym prosić o wyjaśnienie?
3 sty 20:25
===:
|x+3|≠5 czyli x≠−8 x≠2
a miejsce zerowe ....to już banał −
3 sty 20:26
bartosz: Czyli dziedzina to R za wyjątkiem 2 i −8?
3 sty 20:40
Janek191:
Tak
Miejsce zerowe: x = − 3
3 sty 23:59
bartosz: Jak je policzyłeś?
4 sty 00:06
Eta:
Licznik=0 ⇒ x+3=0 ⇒ x=.......
4 sty 00:08
Janek191:
Licznik musi być równy 0 !
x + 3 = 0
x = − 3
=====
4 sty 00:08
bartosz: | | x+3 | |
0 = |
| mnożę przez mianownik |
| | |x+3| − 5 | |
0 = x + 3
x = − 3
Dokładnie tak
4 sty 00:10
bartosz: Zwariuję
4 sty 00:13
Eta:
taaaaaaaaaaaaaaaaaaak
4 sty 00:14
bartosz: Być może zadam głupie pytanie, ale o jakim liczniku mówicie?
4 sty 00:15
PW: Licznik to jest to, co stoi nad kreską ułamkową (a to pod kreską to jest mianownik).
4 sty 00:17
Eta:
| | x+3 | |
y= |
| −−− ułamek algebraiczny |
| | |x+3|−5 | |
x+3 −−− licznik ułamka
|x+3|−5 −−− mianownik
4 sty 00:17
bartosz: No to zrozumiałe.. Ale gdzie on przyjmuje wartość 0 ?
4 sty 00:18
Metis: Zacznij od podstaw
4 sty 00:18
bartosz: No to dobrze zrobiłem
Wymnożyłem przez mianownik, żeby licznik był równy 0!
4 sty 00:18
Eta:
Kiedy ułamek jest równy zero? odpowiedz na to pytanie
4 sty 00:18
bartosz: Metis niepotrzebny komentarz.
4 sty 00:19
Janek191:
Trzeba wrócić do podstawówki
4 sty 00:19
bartosz: Jak licznik jest równy 0. Bo przez 0 nie dzielimy
4 sty 00:19
bartosz: Janek następny
4 sty 00:19
Eta:
Jak licznik =0 i mianownik ≠0
4 sty 00:20
Eta:
Zaraz i ja będę następna
4 sty 00:20
bartosz: Skoro licznik będzie = 0 to po co założenie, że mianownik ma być ≠ 0?
4 sty 00:20
Janek191:
Bo nie wolno dzielić przez 0 !
4 sty 00:21
Eta:
To jest
ułamek algebraiczny , zawiera x zarówno w liczniku jak i w mianowniku
dlatego tak
4 sty 00:22
Janek191:
Inni mówią : " cholero nie dziel przez 0 "
4 sty 00:22
Eta:
"załóż sombrero! i nie dziel przez zero"
4 sty 00:24
bartosz: W gimnazjum byłem asem..
4 sty 00:24
Eta:
Widać po znajomości
4 sty 00:25
bartosz: Mam wrażenie, że jeszcze tu wrócę
4 sty 00:25
bartosz: Ten Wasz cynizm mnie nie dotyka
4 sty 00:26
Eta:
Zapraszamy
na zachętę
4 sty 00:26
Janek191:
A ja Asa zapamiętałem z I klasy . Ala, Ola i As poszli w las
4 sty 00:27
Eta:
Bądź pokorny, to lepiej na tym wyjdziesz
My sobie często tak żartujemy ( nie zrażaj się tym
4 sty 00:27
bartosz: a rozumiem, że państwo tak spędzacie sobotnie wieczory?
4 sty 00:28
Eta:
Dokładnie
nie ma zadań... więc się nudzimy i żartujemy
4 sty 00:29
bartosz: Polecić jakiś film?
4 sty 00:30
Eta: 
Dla Ciebie ( zamiast filmu)
określ dziedzinę i podaj miejsce zerowe tej funkcji
4 sty 00:32
4 sty 00:32
Eta:
Arcy.........
4 sty 00:33
bartosz: Eta, daj mi chwileczkę
4 sty 00:33
Eta:
Nawet ......dwie
4 sty 00:34
kyrtap: 
4 sty 00:35
bartosz: Dziedzina:
x+1 ≠ 0
x ≠ −1
Miejsce zerowe:
0 = 2x−3
4 sty 00:36
Eta: Co
Patryk chciałeś?
4 sty 00:36
kyrtap: Piwko ? Uuuuuuuuuu
4 sty 00:36
Eta:
Bartek
4 sty 00:36
kyrtap: a nic się pokręcę po forum
4 sty 00:36
Janek191:
4 sty 00:37
bartosz: Eta, a moze masz cos z wartoscia bezwzgledna?
Ciekawsze..
4 sty 00:37
Eta:
określ dziedzinę i podaj miejsca zerowe
4 sty 00:39
52: Rozwiąż
a)|x|=−3
b)|x|≥0
c)|x|≤2
d)|x|>−2
4 sty 00:40
bartosz: ETA!
Dziedzina:
x ≠ 3 x ≠ −3
Miejsca zerowe:
x = 5 i x = −3
4 sty 00:45
Janek191:
@Bartosz
4 sty 00:46
Eta:
Bartosz .... miejsce zerowe tylko x= 5 , bo x= −3∉D
4 sty 00:46
Janek191:
To się zagalopowałem z tymi oklaskami
4 sty 00:48
bartosz: Ach, nieuwaga..
4 sty 00:49
bartosz: 52!
a) Niemożliwe jest to co napisałeś
b) x=0
c) x ≤ 2 i x ≥ −2
d) x>−2 i x < 2
4 sty 00:52
Janek191:
@Bartosz
b) źle
d) źle
4 sty 00:54
bartosz: b) x ≥ 0 i x ≤ 0
4 sty 00:56
bartosz: d) nie widzę błędu
4 sty 00:57
Janek191:
@Bartosz
b) x ∊ ℛ
d) x ∊ ℛ
4 sty 01:00
Eta:
a) sprzeczne
b) x∊R
c) x∊<−2,2>
d) x∊R
4 sty 01:00
bartosz: Dlaczego d) R?
4 sty 01:04
Eta:
bezwzględna wartość jest zawsze > −2
4 sty 01:05
Eta:
I jak bartosz ? śpisz?
4 sty 01:12
52: Czyli moje przykłady się przydały widzę
4 sty 01:13
bartosz: Ale R właśnie nie wynika z tego co napisałem u góry, a Janek oznaczył jako złe? x większy od −
2 i x mniejszy od 2, więc wszystkie
4 sty 01:13
Eta: Ty ćwicz lepiej swoje
a nie wyżywasz się na maturzystach
4 sty 01:14
52: Ja chcę dla nich jak najlepiej. Mnie właśnie uczono z takich przykładów dzięki czemu (tak mi
się wydaje ) rozumiem trochę...
4 sty 01:15
bartosz: Eta?
4 sty 01:15
Eta:
W a) napisałeś niemożliwe , czyli sprzeczne , a ładniej : x∊∅
4 sty 01:15
Eta:
w b) napisałeś x=0 a ma być x∊R
4 sty 01:18
bartosz: Mówiłem o d), w b) poprawiłem i wynika to samo o czym mówiłem w poście wyzej
4 sty 01:20
bartosz: Nie łapiesz o co mi chodzi
4 sty 01:20
Eta:
d) |x|>−2 zawsze prawda .......czyli dla x∊R
4 sty 01:22
bartosz: Chyba to dla mnie za późna pora..
4 sty 01:26
4 sty 01:26
bartosz: |x| > 2
x > 2 lub x < − 2
z tego wyszedłem i wyszło mi
|x| > −2
x > −2 lub x < 2
4 sty 01:28
Eta:
Ale Ty masz |x|>−2 a nie |x|>2
Na razie idź do spania
Miłych snów
4 sty 01:28
bartosz: chyba, że mi to wyjaśnisz, ja tymczasem zmykam na breaking bad − dziękuje Eta i Janek, do
usłyszenia
4 sty 01:29
bartosz: No zgadza się, ale analogicznie nie może być tak jak napisałem?
4 sty 01:29
Eta:
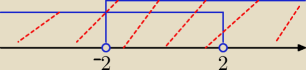
x<2
lub x>−2 ⇒
x∊R
4 sty 01:32
bartosz: NAPISAŁEM TO PRZECIEŻ WCZEŚNIEJ
Tylko darowałem sobie wykres. Jeszcze raz dziękuję
4 sty 01:34
Metis: To nie wykres, tylko os liczbowa i przedziały
4 sty 01:39
Eta:
W takim przypadku zbędne!
Dobrej nocki Wszystkim
4 sty 01:40