Wyznaczyć równanie stycznej do krzywej Maciuś: Wyznaczyć równanie stycznej do krzywej y = f(x) wiedząc, że: a. f(x) = x−6/x+3 oraz styczna tworzy z osią Ox kąt o mierze π/4 b. f(x) = x³−3x²−9x oraz styczna jest równoległa do osi Ox.

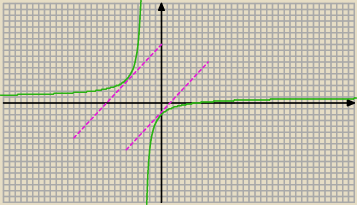
===: a) Styczna ma równanie y=x+b i ma z f(x) jeden punkt wspólny (Δ=0)

x−6
	=x+b ⇒ x−6=x2+bx+3x+3b ⇒ x2+(b+2)x+3b+6=0
x+3

Δ=0 b²+4b+4−12b−24=0 b²−8b−20=0 Δ₁=144 b₁=−2 b₂=10 y=x−2 i y=x+10

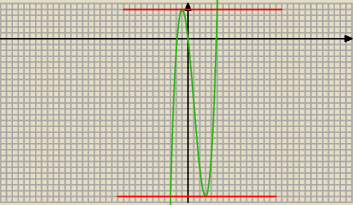
===: b) Zatem pochodna =0 i wyznaczymy iksowe współrzędne punktów styczności f'(x)=3x²−6x−9 f'(x)=0 x²−2x−3=0 Δ=16 x₁=−1 y₁=5 x₂= 3 y₂=−27

pigor: ..., b) f(x) = x³−3x²−9x oraz styczna jest równoległa do osi Ox. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− f'(x)= 3x²−6x−9 i f'(x)=tg0=0 ⇔ 3x²−6x−9=0 ⇔ ⇔ x²−2x−3=0 ⇔ x²+x−3x−3=0 ⇔ x(x+1)−3(x+1)=0 ⇔ ⇔ (x+1) (x−3)=0 ⇔ x= −1 v x=3 ⇒ f(−1)= −1−3+9=5 v f(3)=27−27−27=−27 ⇒ czyli punkty styczności : (−1,5) v (3,−27) , a y−5=0 v y+27=0 − równania stycznych w nich.