geometria analityczna jedrzej123: W zbiorze wszystkich środków okręgów zewnętrznie stycznych do okręgu o równaniu x²+ y² =4 i jednocześnie stycznych do prostej o równaniu 3x−4y−50=0 istnieje okrąg o najmniejszym promieniu. Wyznacz jego równanie.

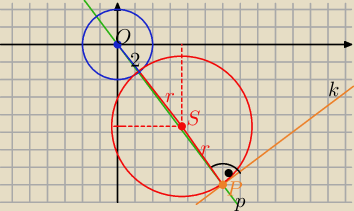
Eta: k: 3x−4y−50=0 o₁ : x²+y²=4 , O(0,0) r₁=2 1/ środek S najmniejszego stycznego okręgu należy do p ⊥k

	4		4
p: y= −		x to S(x, −		x)
	3		3

	|3*0−4*0−50|
2/Odległość "d" O od P ⇒ d=		= 10
	√25

to |OP|=2+2r=10 ⇒ r=4

	16		4
3/ |OS|= 2=r=6 ⇒ x2+		x2= 62 ⇒ xS=...... i yS= −		x=....
	9		3

4/ o₂ : ( x−x_S)²+(y−y_S)²= r² ⇒ o₂ : ................. dokończ obliczenia...........