Geometria na płaszczyźnie Dżepetto 18: Dany jest równoległobok ABCD w którym AC→ = [ 9,3 ] i AB→= [ 4,−2 ]. a) Oblicz pole tego równoległoboku b)wyznacz współrzędne wszystkich wierzchołków równoległoboku, wiedząc, że punkt

	3		1
S = (		, −		) jest jego środkiem symetrii.
	2		2

Niestety nie potrafię zrobić nawet a)

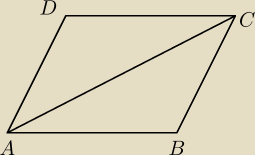
Eve: ten równoległobok składa się z 2 trójkątów

	1
PABC=		Id(AB→,AC→)I
	2

d(...)= wyznacznik wektoró

Dżepetto 18:

	1
Zatem PABC =		|( −18 − 12)| = |−15| = 15 bo na d jest jeszcze nałożona wartość
	2

bezwzględna (|...| odnosiło się wartości bezwzględnej a nie do wyznacznika wektorów )? a) P_ABCD = 2*15=30 j² Dziękuję Eve, połowa już za mną

Eve: nmzc, szukam rozw dob

Eve: AC→[9,3]⇒x_c−x_a=9 i y_c−y_a=3 S − środek symetrii, czyli x_a+x_c=−3 i y_a+y_c=1 ( z własności współrzędnych środka odcinka dostajesz układ równań dla x i y rozwiąż oba otrzymasz współrzędne dla A i C podobnie dla B i D

Dżepetto 18: Eve a czy zamiast x_a+x_c = −3 i y_a+y_c= 1 nie powinno być x_a+x_c= 3 i y_a+y_c= −1? S(1/2 x_a+x_c ; 1/2 y_a+y_c ) a w podanym w zadaniu S znaki "−" są odwrotnie.

Dżepetto 18: Pomyliłaś odrobinkę znaki ale tak to pomysł dobry. Bardzo dziękuję za pomoc