Rachunek różniczkowy Blue:

	1
zad.1 Udowodnij, że dla m≥		funkcja f(x) = x3 −x2+mx−1 jest rosnąca w zbiorze liczb
	3

rzeczywistych. http://i59.tinypic.com/nfsayx.jpg

	4
zad.2 Udowodnij, że funkcja f(x) = x2 +4 +		dla x≠0 przyjmuje wartości niemniejsze od
	x2

8. http://i59.tinypic.com/2wq8xw7.jpg zad.3 Uzasadnij, że równanie x³ −x² −5x+3 = 0 ma trzy pierwiastki rzeczywiste. http://i57.tinypic.com/120p34g.jpg Może tak być udowodnione Wiem, że w tym 3 tak średnio, ale na końcu podałam argumenty dla których są wartości dodatnie i ujemne, więc to powinno wystarczyć, chyba.

Gray: Odnośnie rozwiązania zad. 3 (do którego masz wątpliwości) − ocierasz się o ideał rozwiązania Ja dałbym Ci za to 100%.

kacper: Uzasadnienie pierwszego mnie nie przekonuje

Gray: Ad. 2. Aby uzasadnienie było kompletne, powinnaś zbadać jeszcze jak się funkcja zachowuje na krańcach dziedziny tj. w nieskończonościach oraz w 0.

kacper: Zadanie 2 już kiedyś robiłaś chyba

Maslanek: Do zadania 3 jeszcze istotną informacją byłoby to, że funkcja jest ciągła oraz policzenie granicy w −∞. Nie ma wyjaśnienia, że przed x=−1 funkcja przyjmuje wartości ujemne. Spójrz np. na wykres

	1
funkcji		.
	1+x2

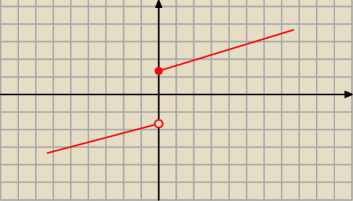
Maslanek: Spodziewam się, że w liceum nie mówi się o twierdzeniu Darboux, ale narysuję Ci pewien rysunek, który pokazuje, że nie zawsze, jeżeli funkcja przyjmuje wartość ujemną i dodatnią, to przyjmie też 0 . Wystarczy nieciągłość w punkcie. Funkcja jest oczywiście ściśle rosnąca i okreslona na zbiorze liczb rzeczywistych

Maslanek: Co więcej przyjmuje wartości ujemne i dodatnie

Gray: "Nie ma wyjaśnienia, że przed x=−1 funkcja przyjmuje wartości ujemne.". Jest.

Maslanek: Aha. Na końcu Spoko Przyzwyczaiłem się do uporządkowanych zapisów

kacper: Zadanie 2

	4
Z nierówności AM−GM dla składników x2 oraz		mamy
	x2

4   x2+   x2		4
	≥√x2*		≥2
2		x2

Zatem

	4
x2+		≥4
	x2

	4
f(x)=x2+4+		≥4+4≥8
	x2

c.n.u Korzystaj z prostych rozwiązań Blue

kacper: Maślanek w podstawie programowej jest zapis "własności funkcji ciągłych". Jak najbardziej ja będę uczniów uczył własności Darboux.

Saizou : Kacper łatwiej nauczyć się schematu pochodnych niż kombinować ze średnimi

Maslanek: Przynajmniej samych faktów związanych z funkcjami ciągłymi. Właśnie, żeby to nie był schemat odwalany bezmyślnie, tylko z pewną świadomością Saizou, ja własności średnich nie ogarniam Nigdy nie robiłem zadań z własności Czasami na pewno dałoby się prościej, ale i tak można

Blue: O jejku, nie spodziewałam się tylu odpowiedzi tak z rana ^^ Dzięki. Ale co Wam nie pasuje w 1 zadaniu?

Blue: Kacper, 2 zadanie kiedyś robiłam podobne, ale nie takie samo

Blue: A w tym 2 co jeszcze dopisać, jeśli chcę to rozwiązać z pomocą pochodnej, a nie średnimi ?

razor:

	4
x2+		+4≥8
	x2

	4
x2−4+		≥ 0
	x2

	2
(x−		)2 ≥ 0
	x

Kacper: Gray ci podał co trzeba zarobić Bo może się okazać, że funkcja ma minimum lokalne równe 8, ale to cały czas minimum lokalne. Nas interesuje wartość najmniejsza (minimum globalne).

Kacper: razor Twoje rozwiązanie najprostsze

Blue: Racja razora najprostsze, ale ja chcę pochodną Czyli mam liczyć granice, czy co?

Kacper: Czytałaś co napisał Gray?

Blue: aa, już chyba wiem, po prostu ta funkcja jest malejąca dla x∊(−∞, √2> i rosnąca dla x∊<√2,∞) to wystarczy

Blue: no i z wykluczeniem 0, bo nie należy do D

Maslanek: Trzeba policzyć jeszcze granice w −∞, +∞, 0⁻, 0⁺. Wtedy jest komplet

Blue: Czyli te granice w nieskończoności wynoszą nieskończoność? i granica w )⁺ i )⁻ = ∞ i jeszcze napisać o tej monotoniczności i to wystarczy?

Blue: granica w 0⁺ i 0⁻ =∞ *?

Maslanek: Tak. Wystarczy policzyć wartości funkcji (lub granice) w nieskończonościach, punktach nieciągłości, punktach stacjonarnych. Przynajmniej tych prostych. Tak się zastanawiam, czy wszystkich Ale chyba tak

Blue: a dobrze mam te granice policzone? Bo nie jestem już pewna czy to tak się liczyło xd

Blue: Czyli te granice to będzie wszędzie nieskończoność?