Planimetria
DropDead: Dwa zewnętrznie styczne okręgi o równych promieniach długości 2 są styczne do prostej k. Trzeci
okrąg jest styczny do prostej k i zewnętrznie styczny do dwóch pierwszych okręgów. Jaka jest
długość promienia trzeciego okręgu?
1 sty 15:15
DropDead: odświeżam.
1 sty 15:41
pigor: ..., np. tak : niech
x=? − szukana dł.promienia "małego"
okręgu w ...

zagłębieniu dwóch danych okręgów i prostą , to
połowa Δ o wierzchołkach w środkach O
1O
2O
3 okręgów jest
Δ prostokątnym o bokach 2,2−x,2+x, więc np. masz równanie z
tw. Pitagorasa
(2+x)2−(2−x)2= 4 ⇔ (2+x−2+x)(2+x+2−x)=4 ⇔
⇔ 2x*4=4 ⇔
x=12 − szukana
długość promienia . ...

1 sty 16:29
DropDead: Zroooobisz rysunek?
1 sty 23:57
panpawel:
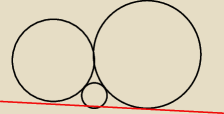
2 sty 00:00
DropDead: To to wiem :v
Nie wiem jak ten trójkąt zbudował.
2 sty 00:12
Eta:
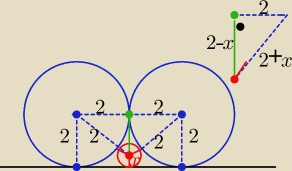
2 sty 00:13
pigor: ..., właśnie tak, ale z małą uwagą, że te 2 "duże"okręgi
mają z warunków zadania
jednakowej długości
promienie...

2 sty 00:16
DropDead: Ooooo dzięki.
2 sty 00:17
pigor: ... no i masz pięknie, prawda


2 sty 00:18
DropDead: Czemu dajesz trzykropek na początku? xd
2 sty 00:19
Eta:
... to dla zamulenia

2 sty 00:20
pigor: ... , no i jak widać mój opis rozwiązania nie był tak bardzo ...

zamulony
2 sty 00:21
Eta:
Jak wstawiłam rys.

to się odmulił
2 sty 00:22
DropDead: No co, dla jednych zadanie jest łatwe bo liczyli podobne milion razy, a drudzy dopiero
zaczynają. :CC
2 sty 00:23
pigor: ..., cóż, dla mnie to pytanie retoryczne, ale jednak ...

masz odpowiedź;
2 sty 00:23
pigor: ..., a tak naprawdę, to mam rysunek zawsze w ...

głowie
co mi wystarcza i wcale nieźle ćwiczy − jak sądzę − wyobraźnię.
2 sty 00:29
 zagłębieniu dwóch danych okręgów i prostą , to
połowa Δ o wierzchołkach w środkach O1O2O3 okręgów jest
Δ prostokątnym o bokach 2,2−x,2+x, więc np. masz równanie z
tw. Pitagorasa (2+x)2−(2−x)2= 4 ⇔ (2+x−2+x)(2+x+2−x)=4 ⇔
⇔ 2x*4=4 ⇔ x=12 − szukana długość promienia . ...
zagłębieniu dwóch danych okręgów i prostą , to
połowa Δ o wierzchołkach w środkach O1O2O3 okręgów jest
Δ prostokątnym o bokach 2,2−x,2+x, więc np. masz równanie z
tw. Pitagorasa (2+x)2−(2−x)2= 4 ⇔ (2+x−2+x)(2+x+2−x)=4 ⇔
⇔ 2x*4=4 ⇔ x=12 − szukana długość promienia . ...






 zamulony
zamulony
 to się odmulił
to się odmulił
 masz odpowiedź;
masz odpowiedź;
 głowie
co mi wystarcza i wcale nieźle ćwiczy − jak sądzę − wyobraźnię.
głowie
co mi wystarcza i wcale nieźle ćwiczy − jak sądzę − wyobraźnię.