Stereometria Blue: zad.1 Kąt dwuścienny między dwoma sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego ma miarę 120⁰. Wykaż, że kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę 45⁰. zad.2 Wykaż, że przekątna BD' prostopadłościanu ABCDA'B'C'D' tworzy z jego krawędziami AB, BC, BB' kąty α, β, γ takie, że cos²α + cos²β + cos²γ = 1. http://i60.tinypic.com/34h8d9k.jpg zad.3 Stożek przecięto płaszczyznami równoległymi do jego podstawy i dzielącymi jego wysokość na n równych części. Udowodnij, że obwody powstałych przekrojów tworzą ciąg arytmetyczny. zad.4 Ostrosłup przecięto dwiema płaszczyznami równoległymi do jego podstawy i dzielącymi jego wysokość na trzy równe odcinki. Udowodnij, że stosunek objętości powstałych brył, licząc od wierzchołka, wynosi 1:7:19. http://i58.tinypic.com/308un7t.jpg http://i58.tinypic.com/14kxm5l.jpg Zadanie 2 i 4 zrobiłam − proszę o sprawdzenie. Proszę o pomoc z zadaniami 1 i 3

Kacper: 1. Dobry rysunek wystarczy 3. Robiłaś bardzo podobne zadanie (ostrosłup był)

Blue: 3. no właśnie wiem, że robiłam, ale tutaj nie ma konkretnej liczby i nie wiem, jak zrobić :c 1. Zrobiłam rysunek i jakoś nie mogę do tego dojść.... A powiesz mi, czy dobrze jest to 2 i 4?

Kacper: Zadanie 2 i 4 dobrze Tam w 3 też nie było konkretnej liczby.

Blue: ale była konkretna liczba tych brył podobnych, które powstaną.

Kacper: No masz ich konkretnie dane: n

Blue: No ale jak ja mam to oznaczyć wszystko, zapisać?

Eta:

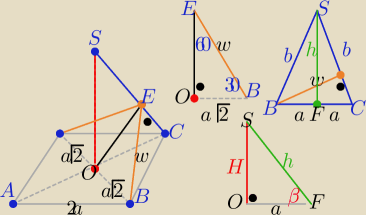
	2a√6		w*b		√6
w=		P(ściany)=a*h=		⇒h=		*b
	3		2		3

	√3
i a2=b2−h2 ⇒ a=		*b
	3

	√3
i H=√h2−a2=............		b
	3

w ΔOFS , H=a ⇒ β=45^o

Eta: Zapomniałam napisać,że zad1.

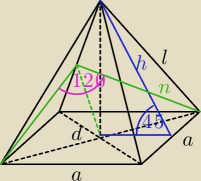
dero2005: d = a√2 d² = 2n² − 2n²cos120^o 2a² = 2n² − 2n²*(−0,5)

	√6
2a2 = 3n2 ⇒ a =		n
	2

n*l = a*h

	√6
n*l =		n*h
	2

	√6
l =		*h
	2

	3
l2 =		h2
	2

l² = (^a₂)² + h²

3		a2
	h2 =		+ h2
2		4

	a√2
h =
	2

a   2		√2
	= cos45o =
h		2

a   2		√2
	=		= cos45o cnd
a√2   2		2

Blue: Dziękuję Eta Jak dla mnie to zadanie było trochę zawiłe

Blue: Może ktoś się pokusi o rozwiązanie 3−ego?

Blue: Pokaże ktoś rozwiązanie do 3 zadania? Bardzoo proszęęę

Kacper: Może niedługo

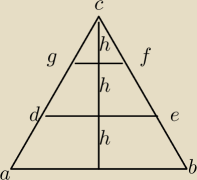
avizelelHLNW: 3 ZAD: Przekrojem jest trójkąt równoramienny, więc |AC| = |BC| Wszystkie trójkąty ABC CDE CGF są podobne zgodnie z cechą kąt−kąt−kąt Jak możemy zauważyć po wysokościach, korzystając z podobieństwa uzyskamy, skalę podobieństwa trójkąta CDE do ABC 2/3 oraz trójkąta CGF do ABC 1/3. Obwód ABC: L= |AB| + 2|AC| Obwód CDE: Lcde= |DE| + 2|DC| , |DE| = 2/3|AB|, |DC|=2/3|AC|, więc Lcde= 2/3L Postępując tymi samymi korkami uzyskamy Lcgf= 1/3L Początkowy wyraz naszego ciągu to cały trójkąt. Kolejne wyrazy do 2/3...1/3.... itd. an= L+2/3L+1/3l+..... <−−− n wyrazów an= a1+(n−1)r r= −1/3L Wzór ogólny ciągu to an=L+(n−1)*(−1/3L)= 4/3L−1/3nL, n∊N≥1 Pamiętajmy, że L możemy potraktować jako liczbę, ponieważ jest to po prostu obwód jakiejś figury. Mogliśmy porzucić cały dowód na etapie policzenia r i stwierdzenia, że jest const. Rysunek czysto poglądowy, lecz tak naprawdę całość opiera się właśnie na nim