pole koła opisanego na prostokącie
mateusz: Pole koła opisanego na prostokącie o bokach długości
√2+1 i
√2−1 jest równe?
30 gru 22:30
Eve: policzyłeś przekątną?
30 gru 22:34
===:
NIE
30 gru 22:36
mateusz: tak, wyszła √6
30 gru 22:39
Eta:
Dobrze!
| | πd2 | |
Pk= |
| , d2=3−2√2+3+2√2=6 |
| | 4 | |
30 gru 22:42
mateusz: Dziękuję ETA
30 gru 22:45
5-latek:
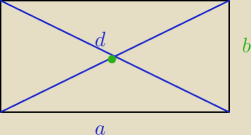
a=
√2+1
b=
√2−1
d
2= a
2+b
2
d
2= (
√2+1)
2+(
√2−1)
2
d
2= 2+2
√2+1+2−2
√2+1
d
2= 6
d=
√6
P
k=pi *r
2
(a to juz sobie policz
30 gru 22:45
Eta:
30 gru 22:46
mateusz: zrobiłem tak jak
5−latek
30 gru 22:47
Eta:
No jak wolisz 10 linijek rozwiązania od 2 linijek
30 gru 22:49
Eta:
Bez
urazy 5−latka .........
na zdrowie
30 gru 22:51
mateusz: To już jest odruch, że liczę r zamiast podstawiać całą przekątną
30 gru 22:51
Eta:
Odruchy, trzeba kontrolować
30 gru 22:52
5-latek: Eta wcale nie czuje urazy
czasami lubie duzo liczyc( a mozna znacznie prosciej i szybciej
30 gru 22:54
mateusz: Teraz przy każdej następnej próbie pomyślę sobie "ohoo, Eta pokazała krótszy sposób, podstawię
przekątną"
Dziękuję i życzę Szczęśliwego Nowego Roku
30 gru 22:55
Eta:
Miło mi ... i tak trzymaj
Szampańskiej zabawy ! ( szampan "Picolo"− bezalkoholowy)
30 gru 22:59
Marcin: a= 2√2
b=2√3
15 maj 11:02