Monotoniczność Ewelina: Zbadaj monotoniczność i ekstremu funkcji:

	x
y=
	lnx

Dawid: Zaczynamy od dziedziny 1.x>0 2.lnx≠0 x≠1 D=(0,1)u(1,∞)

	x		lnx−1
Liczymy y'=(		)'=
	lnx		ln2x

y'=0

lnx−1
	=0
ln2x

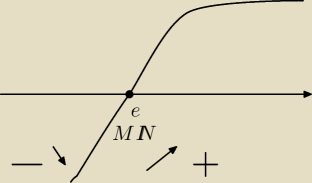
lnx=1 x=e F.maleje od (−∞,e) F.rosnie od (e,∞) Funcja osiąga minimum lokalne w punkcie (e,e) Może ktoś sprawdzić czy dobrze ?

john2: Zapomniałeś tylko o dziedzinie na końcu. Funkcja maleje w przedziale (0,1)∪(1,e) Rośnie w przedziale (e,+∞)