Funkcja wykładnicza, nierówność. Nat: Pomoc w równaniu Rozwiąż nierówność. arcctg(2^x+8 − 4^x−7) < arcctg 40 opuszczam funkcje bo są takie same (?), zamieniam podstawy na dwójkę 2^x+8 − 2^2x−14 < 40 dalej podstawić za 2^x zmienną t? wtedy

	t2
256t −		< 40 ?
	214

w liczniku wyjdzie wtedy liczba 16384, co w późniejszym etapie daje liczby z którymi mój kalkulator sobie nie radzi co robię źle?

Maslanek: Możesz opuścić bo są ciągłe − pytanie tylko czy jest ona malejąca czy rosnąca (w zależności od tego nierówność zmieni znak albo nie). Wiemy, że arcctg jest malejący, więc nierówność zmienia znak! Takich liczb się nie liczy na kalkulatorze (a^x)²=a^2x

Nat: w późniejszym etapie = po przekształceniu na równanie kwadratowe itd

Gray: "Możesz opuścić bo są ciągłe..." − ciągłość nie ma tu znaczenia. Istotna jest jedynie monotoniczność.

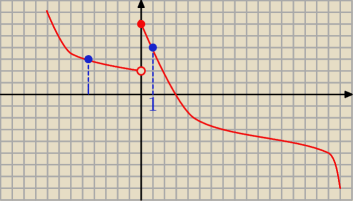
Maslanek: Sprzeczałbym się Rozwiąż nierówność f(x)<f(1)

Gray: Jeszcze jedno (aby nie było wątpliwości): "Wiemy, że arcctg jest malejący, więc nierówność zmienia znak!". Nierówność zmieni znak, bo ctg (a nie arcctg) jest malejący w przedziale (0,π).

Maslanek: Ale ja nie przykładam funkcji ctg, tylko korzystam z monotoniczności. Jeśli chcesz przyłożyć funkcję odwrotną, to raczej powinna być ciągła (być może się mylę, jeśli tak proszę o kontrprzykład)

Gray: Chyba się nie zrozumieliśmy: istotne jest to, że ctg jest malejący (na przedziale (0,π)), a nie że jest ciągły. Gdyby nie był ciągły, rozwiązanie byłoby to samo.

Maslanek: Racja Aczkolwiek monotoniczny w całej dziedzinie

Gray: A mógłbyś pokazać wszystkim jak korzystając z monotoniczności arcctg rozwiązać nierówność: arcctga<arcctgb.

Gray: Funkcja ctg nie jest monotoniczna.