Stereometria Blue: zad.1 Dany jest trójkąt prostokątny. Niech V₁ i V₂ oznaczają objętości brył powstałych w wyniku obrotu tego trójkąta kolejno wokół obu przyprostokątnych, a V₃ − wokół

	1		1		1
przeciwprostokątnej. Wykaż, że		+		=		.
	V1		V2		V3

http://i57.tinypic.com/11qqxcg.jpg http://i58.tinypic.com/m7gc3k.jpg zad.2 W ostrosłupie trójkątnym ABCD krawędź CD jest wysokością i kąty ADB i BED są proste (zobacz rysunek). Udowodnij, że sin²α + sin²β =sin²γ. http://i62.tinypic.com/2kk4nq.jpg zad.3 Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość a. Punkty M i P leżą na wysokości ostrosłupa i |OM|=|MP|, gdzie punkt O jest spodkiem wysokości i O≠P. Przekroje ostrosłupa, równoległe do płaszczyzny podstawy i przechodzące przez punkty M i P mają odpowiednio boki długości b i c. Udowodnij, że ciąg (a,b,c) jest ciągiem arytmetycznym. http://i61.tinypic.com/2e2h0ug.jpg zad. 4 Wykaż, że objętość stożka jest mniejsza od sześcianu długości jego tworzącej . Czy zadanie 1 i 3 może być tak zrobione? I jak zrobić zadanie 2 i 4

:): a dlaczego w 1 masz V² ?

:): 2.

1		1
	DB*AD=		AB*DE
2		2

	CD		CD
sinγ=		⇒DE=
	DE		sinγ

1		1		CD
	DB*AD=		AB*
2		2		sinγ

	AB*CD
sinγ=
	AD*DB

	AB2*CD2
sin2γ=
	AD2*DB2

	CD2		CD2
sin2α=		, sin2β=
	AD2		DB2

	DC2DB2+CD2AD2		CD2(DB2+AD2)
sin2α+sin2β=		=		=
	AD2DB2		AD2BD2

CD2AB2
	=sin2γ
AD2BD2

Blue:

	1		1
zad.1 Sorki, źle przepisałam powinno być tak : Wykaż, że		+		=
	V12		V22

	1
	V32

:): no to masz dobrze

:): w 3 jednak bym pokazała, że to jest ciąg arytmetyczny− wskazała róznicę

:): w 4 nic mi innego nie wpada, jak r<l⇒r²<l² (*) H<l i(*) ⇒ r²*H<l³ (**) 1/3π>1 i (**)⇒V<l³

Blue: To 2 zadanie trochę zawiłe było jak dla mnie Pokażesz jakbyś zrobiła to 3 Rozpiszesz? Zad. 4 Na pewno to jest udowodnione?

:): w 2 nic lepszego nie wymyśliłam w 4 tez mi nic innego nie powychodziło, tylko jakieś bzdury, ale biorąc po uwagę teorię liczb powinno być ok. Może ktos wpadnie na inny pomysł

	a		b		a		c
3		=		i		=
	H		H−x		H		H−2x

policzyłam z tego b i c oraz różnicę a−b i b−c wyszła taka sama

Maslanek: W ostatniej linijce nie wynikać tego wynikania bezpośrednio

Blue: Maślanek, Ty mówić po polsku?

Blue: Może Mila potem coś wymyśli w 4

Maslanek: Nie bardzo dzisiaj Myślę nad tym dowodem

Maslanek: Chciałem powiedzieć, że łatwo to widać geometrycznie, ale wcale nie tak łatwo

Maslanek: Dobra, jest bardzo prosty dowód

Blue: a pokażesz go?

Maslanek:

	pi
Mamy, że 0<x<
	2

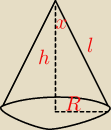
Kolejno:

	1		1		1		π
V=		πr2h=		πsin2x*l2*cosx*l=		πsin2xcosx*l3=		sin2x*sinx*l3<l3, bo:
	3		3		3		6

	π
−		<1
	6

− 0<sin2x<1 − 0<sinx<1

:): a to 4 może tak :

	R3
V=		πsinαcos2α
	3

R=lcosα

	1
V=		l3πcos5αsinα
	3

Maslanek: Kolega uśmieszek przyjął kąt przy podstawie

:): ups, mój błąd sorki cofam dowód

Maslanek: Jest też w porządku Tylko się zastanawiałem, czemu wyszło Ci coś innego niż mi

Blue: Maślanek interesujący dowód

:): własnie tam miał byś lsinα

Blue: A Maślanek mógłbyś jeszcze rzucić okiem, czy to 3 na pewno może tak być?

:): rozpisałam ci 3 17.47

Maslanek: W zadaniu 3 wystarczy pokazać, że 2b=a+c Chyba jest prościej i wtedy zadanie jest na dwie linijki I chyba tak bym to robił Czyli a+c=...=2b

Mila:

	1
V=		πr2*h
	3

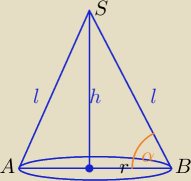
2α<180⁰⇔α<90^o

	r
cosα=
	l

r=l*cosα

	h
sinα=
	l

h=l*sinα

	1
V=		π*l2cos2α*lsinα
	3

	π
V=		*l3*(sinα*cos2α)
	3

	π
V=		*l3*sin(2α)*cosα<l3
	6

f(α)=(sinα*cos²α) możesz poszukać ekstremum.

:): w zasadzie to samo tylko prościej, fakt

Blue: Wiem : ) − i bardzo Ci dziękuję, ale się jeszcze upewniam Maślanek, ale rozwiązanie moje wzbogacone o to, co napisała/ał ; ) chyba też jest poprawnie?

Mila: Przepraszam, przybyli goście i miałam przerwę. Nie było rozwiązań, gdy zaczynałam.

Blue: O Mila, miło Cię widzieć

Blue: : ) − radziłabym Ci zmienić nick, bo gdy ktoś się do Cb zwraca, to nie wiadomo, czy chodzi o emotkę, czy o Ciebie

Eve: ok, pomysłu nie miałam będę sobą czyli

Maslanek: Powiem tyle, że ja z wyjaśnienia, że wysokości tworzą ciąg arytmetyczny nic nie widzę. W zasadzie tyle, że są to założenia zadania. I co z nimi?

Eve: ale wyjaśniliśmy, że a,b,c tez go tworzą z podobieństwa stożków

Blue:

Blue: Maślanek, ale Eve zapisała dopełnienie tego zadania

Maslanek: Z tymi równościami z 17:47 jest w porządku. Ale bez tego samo Twoje ywjasnienie na papierze jest niewystarczające − po prostu zapisałeś założenia

Mila: Tak zrobić, jak pisze Maslanek, 18:23. Ładnie wszystko się zgadza. b i a uzależnić od c,x,u=h₃

Eve: z moich obliczen wynika, że

	ax		ax
b−c=		i a−b=
	H		H

Mila: (a,b,c) c. a. w tej kolejności⇔ b−a=c−b

Eve: ano tak,

Blue: Wiem Maślanek

Kacper:

masochista: Mam pytanko do @Mila, bo jakoś nie mogę ogarnąć ostatniego przekształcenia z 18:23, czy mogłabyś mi to rozłożyć na czynniki pierwsze?

Mila: O to Ci chodzi?

	π
V=		*l3*sin(2α)*cosα<l3
	6

f(α)=(sinα*cos²α)

Mila: sin(2α)*cosα=2 sinα*cosα*cosα=2sinα*cos²

π
	*2sinα*cos2<1 ?
6

π
	*sinα*cos2α<1
3

Masz to wykazać!