Funkcja kwadratowa
Kuba: Na podstawie danych pkt wyróżnionych na wykresie funkcji kwadratowej f wyznacz wzór tej funkcji
w postaci iloczynowej, a następnie podaj jej wzór w postaci ogólnej i kanonicznej. Podane pkt
to : (−2,−2) (0, 0), (0, 3)
29 gru 22:33
:):
ułóż układ równań
ax2+bx+c=0
wstaw współrzędne, rozwiąż
29 gru 22:36
:):
nie może być (0,0) i (0,3) bo to nie jest funkcja
29 gru 22:39
===:
... bzdura
29 gru 22:41
Kuba: Pomoże ktoś ?
29 gru 22:54
Mila:
Każdej liczbie x∊D ma odpowiadać dokładnie jedna wartość, a Ty podałeś, że dla x=0 wartość 0 i
dla x=0 wartość 3.
Popraw treść.
29 gru 22:57
Kuba: Ale tak jest w treści tzn mam do tego rusunek na ktorym zaznaczony jest pkt (−2,−2) i 2 miejsca
zerowe
29 gru 23:03
Mila:
Jakie są te miejsca zerowe?
29 gru 23:07
Mila:
x1=..?
x2=.. odczytaj na osi OX.
29 gru 23:08
Kuba: aaa faktycznie zrobiłem błąd przepraszam miało być (3,0)
29 gru 23:09
Mila:
Czyli os OX przecięta w punktach(0,0), (3,0) Tak?
29 gru 23:12
Eta:
| | 1 | | 3 | |
y= − |
| x2+ |
| x −−− postać ogólna |
| | 5 | | 5 | |
| | 1 | | 3 | | 9 | |
y=− |
| (x− |
| )2+ |
| −−− postać kanoniczna |
| | 5 | | 2 | | 20 | |
29 gru 23:17
Kuba: Ale jak to obliczyć ? nie zalezy mi na wyniku tylko na tym jak do niego dojsc
29 gru 23:19
Eta:
Z postaci iloczynowej:
| | 1 | |
y=ax(x−3) i P(−2,−2) ⇒ −2=a*(−2)(−2−3) ⇒ a= − |
| |
| | 5 | |
| | 1 | | 1 | | 3 | |
y= − |
| x(x−3) ⇒ y= − |
| x2+ |
| x |
| | 5 | | 5 | | 5 | |
| | x1+x2 | | 3 | | 3 | |
xw= |
| = |
| to yw= f( |
| )=.......... |
| | 2 | | 2 | | 2 | |
y= a(x−x
w)
2+y
w = ............
dokończ..........
29 gru 23:28
Mila:
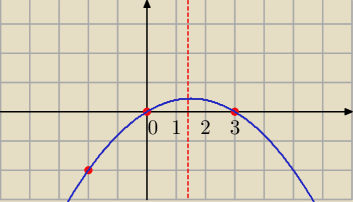
x
1=0, x
2=3
f(x)=a*(x−0)*(x−3) i f(−2)=−2 postać iloczynowa
Obliczamy a
f(x)=−2=a*(−2)*(−2−3)⇔
10a=−2
| | 1 | |
1)f(x)=− |
| *x*(x−3) postać iloczynowa |
| | 5 | |
==================
2) Postać kanoniczna
| | 0+3 | | 3 | |
xw= |
| = |
| odcięta wierzchołka paraboli, podstawiamy do wzoru f(x) |
| | 2 | | 2 | |
| | −1 | | 3 | | 3 | | 9 | |
yw= |
| * |
| *( |
| −3)= |
| sprawdź |
| | 5 | | 2 | | 2 | | 20 | |
| | 1 | | 3 | | 9 | |
f(x)=− |
| *(x− |
| )2+ |
| postac kanoniczna |
| | 5 | | 2 | | 20 | |
3) postac ogólna wymnóż w postaci iloczynowej.
29 gru 23:29
Kuba: Dziękuję bardzo
29 gru 23:34
Eta:
Jeżeli y= ax
2+bx+c
| | −b | | b | |
xw= |
| to yw= c−a*xw2 lub yw= c+ |
| *xw |
| | 2a | | 2 | |
| | 1 | | 3 | |
w tym przykładzie y= − |
| x2+ |
| x |
| | 5 | | 5 | |
| | 3 | | 1 | | 9 | | 9 | |
xw= |
| to yw= |
| * |
| = |
| |
| | 2 | | 5 | | 4 | | 20 | |
| | 1 | | 3 | | 9 | |
postać kanoniczna : y= − |
| (x− |
| )2+ |
| |
| | 5 | | 2 | | 20 | |
30 gru 01:38
Madzia: @Mila Jak obliczyć tą postać iloczynową ?tzn skąd wiadomo którego wzoru uzyc ?
30 gru 11:21
J:
postać iloczynowa: f(x) = a*(x − x1)*(x − x2) ... gdzie: x1 i x2 to miejsca zerowe ...
30 gru 11:42