wzory na matma: Mógłby mi ktoś podać wzory na wysokości trójkątow prostokatnych rownoramiennych i na pole i na promień.Z Góry dziękuje

:): wysokości to przyprostokątne

:): b²=h²+y² h²=a²+x² x+y=c

bezendu: google nie gryzie

:): * a²=h⁺x² sorki

Eta:

:): reszta należy do ciebie, i jaki promień chcesz?

matma: Wzor na promień trójkąta rownoramiennego

Eta: promień

bezendu: Ale to jest słońce ?

:): ja pierwsze słyszę o takim promieniu

Lukas: Eta jak po świętach ? Rózga była ?

Lukas: Hahah

Lukas: Grzeczny byłem

Mila: Chłopcy to grzeczni są po 50−tce. Wtedy należy parzyć im ziółka.

Lukas: Do matury w maju

Eta: Hej Mila Po 50−tce? marudni,jak ......

Lukas: po 40 człowiek ma

kyrtap: Kobiety są też marudy

matma: Wracajac do tematu jak mamy okrąg wpisany w trójkat rownoramienny to jak mamy go obliczyć ten promień okręgu? Mowicie że niema takiego promienia a tu jednak jest

Mila: Wyrażasz się nieściśle. Pytałeś o promień trójkąta równoramiennego. Nie ma czegoś takiego. Możesz pytać o promień okręgu wpisanego w trójkąt. Możesz pytać o promień okręgu opisanego na trójkącie. Nie ma co uczyć się wszystkich wzorów na pamięć. Masz rozumieć problem. Teraz napisz konkretne zadanie z podręcznika.

matma: Pole trójkąta rownoramiennego wynosi 38. W ten trójkąt wpisano okrąg o polu 6 pi a podstawa ma 4cm.Oblicz promień okregu i ramie trojkąta

Wielomian: Nijak to wszystko ma się do siebie. Dobrze przepisałaś/eś treść zadania?

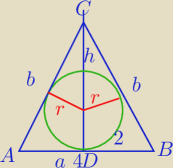
Mila: P_Δ=38

	1
PΔ=		a*h⇔
	2

	1
38=		*4*h
	2

38=2*h h=19 WΔCDB z tw. Pitagorasa: b²=2²+19² b²=4+361 b²=365 b=√365 ramię Δ P_koła=6π⇔ 6π=πr² r²=6 r=√6 To coś jest xle w treści, bo nie zgadza się to pole . Do jutra, już opuszczam forum.

pigor: ..., Mógłby mi ktoś podać wzory na wysokości trójkątów prostokątnych równoramiennych, na ich pole i na promienie okręgów wp(op)isanych . −−−−−−−−−−−−−−−−−−−−−−− oto odpowiedzi na pytania w treści zadania: i tak, jeśli a,a,a√2 − długości 3−ech jego boków (2−ie przyprostokątne i przeciwprostokątna) , to h₁=h₂=a i h₃ = ¹₂a√2 − długości 3−ech jego wysokości , P=¹₂a² − pole trójkąta prostokątnego równoramiennego (połowy kwadratu), r= ¹₂(a+a−a√2)= ¹₂a(2−√2) − dł.promienia okręgu wpisanego , R= h₃ = ¹₂a√2 − dł. promienia okręgu opisanego na tym trójkącie. ...