GEOMETRIA Blue: Czy ja to udowodniłam a) Trójkąty ACH i BCH są przystające, bo mają ten sam bok |CH| i |AH|=|BH| oraz kąt AHC = kąt BHC (mogę założyć, że te kąty są takie same?) . Zatem |AC| = |BC|, czyli trójkąt ABC jest równoramienny. b) Trójkąt CDE jest równoramienny, zatem kąt CDE = kąt CED. Trójkąty CDB i CEA są przystające na podstawie cechy BKB − |DB|= |EA| i |DC|= |CE| oraz kąt CDB= kąt CEA. Skoro te trójkąty są przystające, to |AC|=|BC|, czyli trójkąt ABC jest równoramienny . Może tak być Oto zadanie: http://i59.tinypic.com/30ctwsn.jpg

:): b) w porządku w a) zastanawiam sie nad tymi kątami

Saizou : tak bo AGBH jest deltoidem

:): AHG i BHG też są przystające, spróbuj na podstawie tego wykazać równość tych katów w a)

panpawel: a) To przystawanie wynika z faktu, że na AGBH możemy opisać okrąg i łuk AH w HB, czyli kąt AGH = kąt GHB. (kbk)

panpawel: łuk AH=HB*

Blue: ok, dzięki

Blue: ale chyba tak, jak mówi też by mogło być

panpawel: Ale to, że jest deltoidem też trzeba udowodnić.

:): no tak, czworokąt o sasiednich bokach równych, naprzeciwległych kątach równych , w najgorszym razie musi byc deltoidem, nie ma innej możliwości

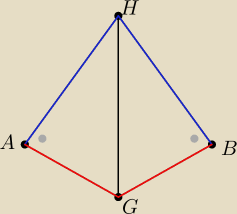
Saizou : AH=BH z treści zadania GH jest przeciwprostokątną ΔAGH i ΔHBG czyli AG=GB