Narysuj zbiór spełniający podany warunek w płaszczyźnie zespolonej Freyja: Mógłby mi ktoś może pomóc z takim zadaniem? Re(z³) ≥ 0 podstawiam z = x + yi, podnoszę do trzeciej potęgi, wypisuję wszystkie wyrazy bez "i" i otrzymuję takie coś: x³ − 3xy² ≥ 0 i nie za bardzo wiem co dalej z tym począć? Być może ja w ogóle źle podchodzę do zadania i powinnam spróbować z postacią trygonometryczną? Ale jeśli tak, to czy ktoś mógłby objaśnić co i jak tam działa, bo tamtej metody już zupełnie nie rozumiem?

:): x+yi=IzI(cosα+isinα) IzI=√a²+b²

	a		b
cos=		, sin=
	IzI		IzI

Freyja: okej, podnoszę z do trzeciej wg wzoru z postacią trygonometryczną i dochodzę do takiego momentu: |z|³cos3α≥0, a że |z|³ jest zawsze większe lub równe 0, to zostaje: cos3α≥0 I z tym już nie mam pojęcia co począć?

Mila: x³ − 3xy² ≥ 0 ⇔ x*(x²−3y²)≥0⇔ x*(x−√3y)*(x+√3y)≥0⇔ 1) x≥0 i x≥√3y i x≥−√3y≥0⇔

	x		x
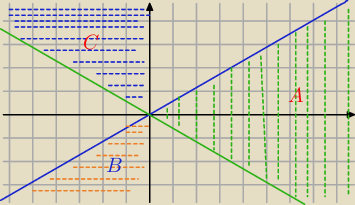
x≥0 i y≤		i y≥−		obszar A
	√3		√3

lub 2)x≤0 i x≥√3y i x≤−√3y⇔

	x		x
x≤0 i y≤		i y≤−		obszar B
	√3		√3

3)x≤0 i x≤√3y i x≥−√3y

	x		x
x≤0 i y≥		i y≥−		obszar C
	√3		√3

Freyja: pięknie dziękuję

Mila: