zadania maturalne Julia: 1.Wykaż, że dla każdej liczby naturalnej n reszta z dzielenia kwadratu liczby 2n +3 przez 8 jest równa 1. 2. W trójkącie ABC środkowa Cs jest prostopadła do dwusiecznej AK. Wykaż, że jeden z boków trójkąta jest dwa razy dłuższy od jednego z pozostałych. 3.W trapezie równoramiennym długość krótszej podstawy jest równa długości ramienia, a przekątna jest prostopadła do ramienia. Oblicz miary kątów trapezu. 4. Wyznacz równanie prostej, która przechodzi przez punkt A=(2,4) i jest równo oddalona od punktów B=(−1,1) i C=(3,−1). Rozważ dwa przypadki. Ps.Tak gdzie to możliwe poproszę o rysunek

Eta: 1/ L=(2n+3)²= 4n²+12n+9= 4(n²+3n+2)+1= 4*(n+1)(n+2) +1 = 8*k+1, k∊N bo ............... dodaj odpowiedni komentarz

Julia: bo (n+1) i (n+2) to liczby naturalne czyli jest 8k+1, tak?

Julia: a co z resztą, ktoś coś?

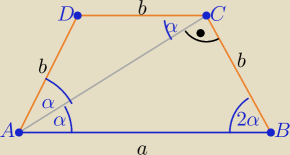
Eta: zad3/ Rys. wyjaśnia ....( podaj uzasadnienie α+2α=90^o ⇒ α=...... |∡A|=|∡B|=...... i |∡D|=|∡C|=..........

Eta: @Julia .... niestety,ale to nie jest dobry komentarz Podaj jeszcze raz, ale poprawny komentarz

Eta: "Co z resztą" ? myśl też troszkę sama

bezendu:

Julia: kurczaki, no nie wiem jaki jest dobry komentarz do tego zadania. a 3 mam tak: α=30 |∡ ADC= |∡ DCB= 60, bo to jest 2α a |∡adc i |∡cba mają po 120, bo 360−120=240/2=120 a reszty tak na serio nie wiem

Julia: ale za to mam 4 wyznaczam równanie prostej bc 1=−a+b=> b=1+a −1=3a+b a=−1/2 b=1/2 y=−1/2x+1/2 przypadek 1. prosta jest prostopadła do prostej y=−1/2x+1/2 4=−1/2 *2 +b b=5 y=−1/2x+b 2 przypadek prosta nie jest prostopadła, ale przechodzi przez środek prostej bc x=−1+3/2= 1 y=1−1/2=0 (1,0) (2,4) 0=a+b =>b=−a 4=2a+b 4=2a−a a=4 b=−4 y=4x−4 Dziękuję za uwagę

Julia: no a zadania typu wykaż, że to dla mnie kosmos

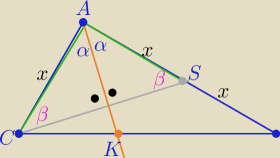
Eta: zad.2/ Trójkąt ACS jest równoramienny o ramionach |AC|=|AS|=x ,x>0 i |AB|=2x ⇒ |AB|=2|AC| c.n.u