. maturaa: Uzasadnij, że jeżeli α jest katem ostrym, to sin⁴α+cos²α=sin²α+cos⁴α

:): przenieś cos⁴ na lewo, sin² na prawo rozpisz lewą ze wzorów skróconego mnożenia

Gray: A może tak: Lewa=sin⁴α+cos²α=sin⁴α+(sin²α+cos²α)cos²α = sin⁴α + sin²α cos²α + cos⁴α = =sin²α(sin²α+cos²α) + cos⁴α = sin²α + cos⁴α=Prawa Koniec

Gray: I tradycyjne pytanie: gdzie korzystamy z tego, że kąt α jest ostry?

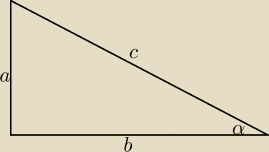
Bogdan: można i tak:

	a		b
α∊(oo, 90o), sinα =		, cosα =		, a2 + b2 = c2
	c		c

	a4		b2		a4 + b2c2
sin4α + cos2α =		+		=		=
	c4		c2		c4

	a4 + b2(a2 + b2)		a4 + a2b2 + b4		a2(a2 + b2) + b4
=		=		=		=
	c4		c4		c4

	a2c2 + b4		a2		b4
=		=		+		= sin2α + cos4α
	c4		c2		c4