zadanie Blue: Przekrój ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez jego wierzchołek i przekątną podstawy jest trójkątem równobocznym o polu równym 9√3. Objętość tego ostrosłupa jest równa: A.36√3 B.72√3 C.18√3 D.54√3 Mi wyszło C, ale w odpowiedziach mam A, więc już nie wiem..........

:): a=6, H=3√3

Blue: a skąd Ty wzięłaś to a=6? Czy krawędź podstawy nie będzie wynosić 3√2

J: mnie też wyszło C ...

J: krawędź podstawy a = 6 ...

Blue: ale ja mówię o krawędzi podstawy ostrosłupa

J: sorry ... krawędź a = 3√2 ...

Blue: Czyli na pewno jest błąd w odpowiedziach , tak?

J: tak .. krawędź podstawy : a = 3√2

:):

	a2√3
9√3=
	4

:): fakt, sorki, a to przekatna, krawędź 3√2 zatem błąd w odp

J:

	1		6√3
V =		(3√2)2*		= 18√3
	3		2

Blue: Dzięki

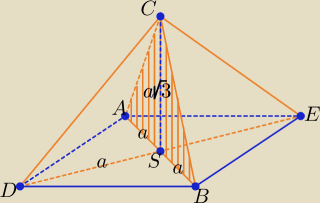
Bogdan: Można i tak zobaczyć ten ostrosłup: Tu są dwa ostrosłupy ABCD i ABCE o wspólnej podstawie ABC, wysokość każdego z nich jest równa a. a*a√3 = 9√3 ⇒ a = 3

	1
V = 2*		*9√3*a = 18√3
	3