dowody Blue: zad.1 Środkowe AD i A1D1 poprowadzone odpowiednio w trójkątach ABC i A1B1C1 mają równe długości. Wykaż, że jeśli: a) |AB|=|A1B1| i |BC|=|B1C1|, to |AC|= |A1C1| http://i61.tinypic.com/3536u6v.jpg b) kąt CAD= kąt C1A1D1 oraz kąt ADB = kąt A1D1B1, to |AB|=|A1B1| zad.2 Punkt P należy do przekątnej AC równoległoboku ABCD (patrz rysunek). Wykaż, że pola trójkątów ADP i ABP są równe. http://i60.tinypic.com/9iusyr.jpg http://i59.tinypic.com/3509v2f.jpg Może tak być wyjaśnione to 1 a) i 2 I jak zrobić to 1b)

:): 1b) ACD=A1C1D1 i ADC=A1D1C1⇒(z wł. kata zewnętrznego) ACD=A1C1D1 ΔACD przystaje doΔA1C1D1 (kbk)

:): 2. mozna zapisać symbolami P(ABC)=P(ADC) − wł. równoległoboku 1/2AC*DD₁=1/2AC*BB₁⇒DD₁=BB₁ P(ADP)=1/2AP*DD₁ ⇒P(ADP)=P(ABP) P(ABP)=1/2AP*BB₁

Blue: Mógłby ktoś może to b) wyjaśnić z rysunkiem Bo nie za bardzo rozumiem I czy może być tak to 1 a) i 2 czy niekoniecznie?

:): jak bym miała oceniać, to wolałabym, żeby 2 rozpisane było wzorami zaraz ci rozrysuje 1b, tylko znajde kartkę

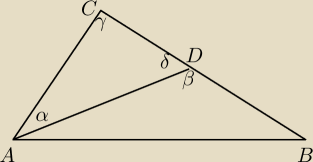
:): β=α+γ, tak samo w drugim Δ, δ jest równy tamtemu δ AD=A1D1 , więc masz ceche przystawania kbk ad, α ,δ

:): CD=BD, z przystawania ACD i A1C1D1 masz DB=D1B1 − AD środkowa z cechy bkb − AD, β , BD i odpowiednie w drugim − masz AB=A1B1

Blue: ok, czyli jak te dwa mniejsze trójkąty są przystające, to z tego też wynika, że cały jest przystający w tym przypadku, już rozumiem

Blue: Dzięki

:): uff, myślałam, że zagmatwałam