Oblicz Smog: Proszę o pomoc w rozwiązaniu. Z góry Serdecznie Dziękuje 1 Sprawdź czy nieskończony ciąg ( aⁿ ), jest monotoniczny, jeśli: a) a_n = (−1) ^2_n+1 b) a_n = (n+4)² 2 Dany jest ciąg arytmetyczny ( a_n ) określany wzorem rekurencyjnym a₁=−7 a_n=a_n−1=3 ( te dwa ciągi sa połączone z przodu nawiasem) a) Wyznacz siódmy wyraz tego ciągu b) Czy jest to ciąg malejący, rosnący czy stały ? 3) Wyznacz pierwszy wyraz i różnicę ciągu arytmetycznego, którego a₁₃ = 0 , a₂₉ = 8 4) Wyznacz ogólny wyraz ciągu geometrycznego ( a_n) , wiedząc, że a₅ =−1 , a₈ =−⁸₂₇ . Zbadaj monotoniczność tego ciągu. 5) Określ stopień jednomianu : a) f(x) = √3 (x⁴) ³ × x⁷ b) g(x) = 0,2 × xⁿ 6) Wyznacz W(x) + P(x), W(x) − P(x) oraz W(x) × P(x), jeśli: a) W(x) = 3 x⁵ − 4 x³⁺⁵ , P(x)=−7 b) W(x) = − x⁴ − 2 x³ , P(x) = x³ −4x 7) Które z liczb należących do zbioru {−4, −√2 , −1, 1, √2 , 3 } są pierwiastkami wielomianu W(x) = x⁴ − 3 x² + 2² 8) Sprawdź, czy funkcje określone wzorami są funkcjami homograficznymi : a) F(x) = ^4x+8_x+2 b) G(x) = ^3x−6₂ 9) Narysuj wykres funkcji 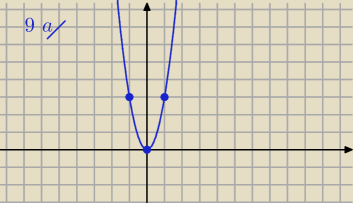a) y= 3 x² 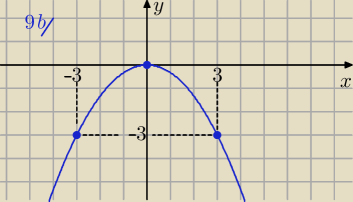b) y= −¹₃ x² c) y= x² − 3x+4 10) Rozwiąż równanie: a) 3x⁴ + 3x² − 6 = 0 b) x² − 3x − 7 = 0 c) x² − 11x+28 = 0 Bardzo Was proszę o Pomoc. Jest mi to Bardzo potrzebne.

Eta: Jakby było tych zadań 50 , to tak

Smog: Yhm, Czyli za mało mi zadają heh Potrzebne mi jest to na prace semestralna a nie mogę sobie z tym poradzić

Mila: Rozwiązuj po kolei, będziemy podpowiadać, wyjaśniac.

Eta: 10/ a) 3x⁴+3x²−6=0 /;3 x⁴+x²−6=0 ⇒ (x²+3)(x²−2)=0 ⇒ (x²+3)(x−√2)(x+√2)=0 ⇒ x=√2 v x= −√2 b) x²−3x−7=0 , Δ= 9+28= 34 , √Δ=√34

	3+√34		3−√34
x=		v x=
	2		2

c) x²−11x+28=0 ⇒ (x−7)(x−4)=0 ⇒ x=7 v x= 4

Eta: 7/ W(x)= x⁴−3x²+2=(x²−1)(x²−2)= (x−1)(x+1)(x−√2)(x+√2) Pierwiastkami rzeczywistymi tego wielomianu są : x={−1, 1, −√2, √2}

Smog: Bardzo Pani dziękuje za rozwiązanie. Byłem przekonany że w 10 wszystkie 3 trzeba rozwiązać przy pomocy funkcji kwadratowej, i bym się pomylił

Ajtek: Smog bo trzeba .

Eta:

Eta:

Eta:

Smog: Bardzo Wam Dziękuje

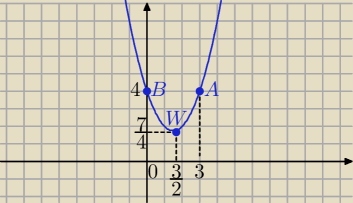
Eta: 9c) y=x²−3x+4 , a=1, b= −3 , c=4 , Δ= 9−16= −7

	−b		3		1		−Δ		7		3
xW=		=		=1		, yW=		=		=1
	2a		2		2		4a		4		4

do wykresu należą punkty : A(3,4) , B(0,4)

Smog: Dziękuje Pani Bardzo. Sam bym sobie z tym nie poradził.

Mila: 1)Sprawdź czy nieskończony ciąg ( a_n ), jest monotoniczny, jeśli: a) a_n=(−1)²ⁿ⁺¹ 2n+1− liczba naturalna nieparzysta , n∊N₊ Zatem (−1)²ⁿ⁺¹=−1 dla każdego n∊N₊⇔jest to ciąg stały. Przykłady kilku wyrazów: a₁=(−1)^2*1+1=(−1)³=−1 a₂=(−1)^2*2+1=(−1)⁶=(−1) O ile dobrze odczytałam zapis ciągu.

Mila: Lapsus: (−1)⁵=(−1)

Eta: 8/ dla x≠ −2

	4x+8		4(x+2)
f(x)=		=		= 4 −−− funkcja stała( nie jest homograficzną)
	x+2		x+2

	3x−6		3
g(x)=		=		x−3 −−−− funkcja liniowa( też nie jest homograficzną)
	2		2

Eta: 5/a f(x)= √3*x¹²*x⁷= √3x¹⁹ −−− jest st.19 b) g(x)=0,2xⁿ −−− jest st. n

Eta: zad 6/ spróbuj samodzielnie zobacz tu : https://matematykaszkolna.pl/strona/1434.html

Mila: 1) b) a_n = (n+4)² a_n+1=(n+1+4)²=(n+5)² Badamy znak różnicy : a_n+1−a_n=(n+5)²−(n+4)² =n²+10n+25−(n²+8n+16)= =n²+10n+25−n²−8n−16=2n+9>0 dla n∊N₊⇔ciąg jest monotoniczny − ciąg rosnący. II sposób Możesz to zbadać rysując wykres funkcji kwadratowej: f(x)=(x+4)² Dla x≥−4 funkcja rosnąca, zatem dla x∊N₊funkcja rosnąca⇔ciąg jest rosnący.

Smog: Bardzo Panią Dziekuje. Ratujecie mi życie

Mila: Paniom. ( Będzie jeden błąd mniej z j. polskiego)

Smog: Ups Sorki. To pewnie z pośpiechu, jestem troszkę zdenerwowany. Tak czy siak Panią czy Paniom i tak Baaardzo Dziękuje.

Eta: 3/ W ciągu arytmetycznym a₁₃=0 , a₂₉=8 to

	a29−a13		8		1
r=		=		=
	29−13		16		2

a₁= a₁₃−12r= 0−6= −6

Mila: Dobranoc.

Smog: Dobranoc. Jeszcze raz bardzo dziekuje

Eta: Dobrej nocki

Smog: Mam nadzieję. Muszę się z tą nieszczęsną matma uporać

Lukas: Eta się jednak skusiła słaba wola

Smog: Nie słaba wola, tylko Dobre Serce

Lukas: Czasami za dobre

Smog: Dobrze że tym razem było "...za dobre" bo bym poległ. Ale tak to jest jak kto ma czache nie przystosowana to cyferek

Eta: 2/ { a₁=7 { a_n=a_n−1+3 a₂= a₁+3= 7+3=10 a₃= a₂+3= 10+3=13 to r= 3 i a₁=7 a₇=a₁+6r= 7+18=25 ciąg {a_n} : 7,10,13,16,.... jest rosnący

Smog: Bardzo dziękuje Pani za kolejne rozwiązanie Życzę Miłego Dnia