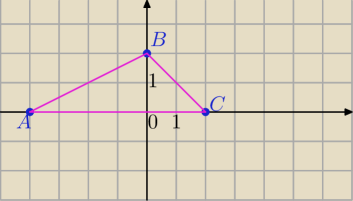
calka zadanie: Obliczyc: ∫∫(1+x−y)dxdy, gdzie R jest trójkątem o wierzchołkach A=(−4,0),B=(0,2),C=(2,0) R W odpowiedzi jest 2. Mi wychodzi −2. Robilem dwoma sposobami tzn. raz wzgledem osi x a raz wzgledem osi y i w obu wyszlo −2. Moze robie blad?

Mila: Rozwiążę:

Mila: AB: AB^→=[4,2]

x+4		y−0
	=		⇔
4		2

A=(−4,0)

	1
AB: y=		x+2
	2

BC^→[2,−2] C=(2,0)

	x−2		y
BC:		=
	2		−2

y=−x+2 ₋₂∫⁰[₀∫^0.5x+2(1+x−y)dy]dx+₀∫²[₀∫^−x+2(1+x−y)dy]dx= tak liczyłeś?

Mila: Oczywiście w pierwszej całce dolna granica −4. Też mi wychodzi (−2).

zadanie: Tak było liczone i jeszcze w drugą stronę. Czyli wychodzi (−2). Dziękuję.

Mila: