.
wercia: dane jest wyrażenie W=|2x−10|−|x+2|. Zapisz wartość wyrażenia bez symbolu wartości
bezwzględnej.
27 gru 16:01
Jolanta: a w takim przykładzie umiesz zapisac ?ale nie licz
|2−6|=
27 gru 16:06
27 gru 16:06
Kasia: 2x−10 − x + 2 = 0 −2x+10 + x +2 = 0
x − 8 = 0 −x + 12 = 0
x = 8 lub x = 12
27 gru 16:12
Jolanta: Nie
Wercia jezeli chcesz pomocy to odpowiedz na pytanie
27 gru 16:17
wercia: hmm |2−6|.. nie za bardzo wiem o co chodzi.. Jolu jeśli masz czas to mogłabyś mi jakoś to
wyjaśnić?

27 gru 16:19
Jolanta: tak
a umiesz to wyliczyć ?
27 gru 16:20
wercia: tak, chyba umiem

27 gru 16:21
Jolanta: czyli mamy |−4| =4 tak ?
27 gru 16:22
pigor: ..., miejsca zerowe wyrażeń pod modułem to −2 i 5, zatem rozpatruję :
W=|2x−10|−|x+2| , gdy (x<−2
v −2≤ x< 5
v x ≥5) , wtedy wyrażenie
(W=−2x+10+x+2 i x<−2)
v (W=−2x+10−x−2) i −2≤ x<5)
v (W=2x−10−x−2) i x ≥5) ⇔
{ − x+12 , gdy x<−2
W= { −3x+8 , gdy −2≤ x< 5
{ x−12 , gdy x ≥5 . ...

27 gru 16:24
wercia: no tak bo wartość wartosć bezwzględna na minusie daje liczbę dodatnią
27 gru 16:25
Jolanta: jeżeli wychodzi ci minus to zmienisz znaki
|3−7|=−3+7=4 jasne ?
jeżeli wychodzi plus nic nie zmienasz
|6−2|=6−2
|2+4|=2+4
można dalej ?
27 gru 16:36
Gray: A taka odpowiedź jest OK?
... = √(2x−10)2 − √(x+2)2
Zapewne tak, bo wartości bezwzględnej nie ma...
27 gru 16:39
pigor: ..., oczywiście jeśli widzimy
różnicę w zapisach
√x2 ≠
√x2=(
√x)
2...

27 gru 19:01
Mila:
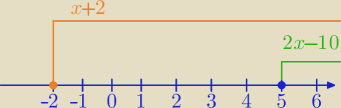
W=|2x−10|−|x+2|
|2x−10|=2x−10 dla 2x−10≥0 ⇔dla x≥5
|2x−10|=−(2x−10)=−2x+10 dla x<5
|x+2|=x+2 dla x+2≥0 czyli dla x≥−2
|x+2|=−(x+2)=−x−2 dla x<−2
1)x<−2 wtedy
W=−2x+10−(−x−2)=−2x+10+x+2=−x+12
2) x∊<−2,5)
Próbuj dalej sama.
27 gru 23:52




 W=|2x−10|−|x+2|
|2x−10|=2x−10 dla 2x−10≥0 ⇔dla x≥5
|2x−10|=−(2x−10)=−2x+10 dla x<5
|x+2|=x+2 dla x+2≥0 czyli dla x≥−2
|x+2|=−(x+2)=−x−2 dla x<−2
1)x<−2 wtedy
W=−2x+10−(−x−2)=−2x+10+x+2=−x+12
2) x∊<−2,5)
Próbuj dalej sama.
W=|2x−10|−|x+2|
|2x−10|=2x−10 dla 2x−10≥0 ⇔dla x≥5
|2x−10|=−(2x−10)=−2x+10 dla x<5
|x+2|=x+2 dla x+2≥0 czyli dla x≥−2
|x+2|=−(x+2)=−x−2 dla x<−2
1)x<−2 wtedy
W=−2x+10−(−x−2)=−2x+10+x+2=−x+12
2) x∊<−2,5)
Próbuj dalej sama.