PLANIMETRIA
agent0013: 1. w trójkącie równobocznym ABC na boku BC wybrano taki punkt P, że |BP| : |PC|=1:2. oblicz
tangens kąta PAB.
2.W trójkącie prostokątnym ABC, w którym kąt przy wierzchołku C jest prosty i |AB| =8,
dwusieczna kąta A i środkowa CD przecinają się pod kątem prostym w punkcie K. Wyznacz długość
odcinka BK.
3. Dany jest trójkąt prostokątny ABC, w którym kąt przy wierzchołku C jest prosty i |AC|>|BC|.
Środek okręgu stycznego do boku BC w punkcie E i do boku AC w punkcie D leży na
przeciwprostokątnej i dzieli ją na odcinki o długościach 15 i 20.
a)oblicz długość promienia tego okręgu
b) Proste AB i DE przecinają się w punkcie P. Oblicz długości odcinków PB i PE.
27 gru 15:25
pigor: ..., np. tak : niech |∡PAB|=x, to z warunków zadania
1. sinx : sin(60o−x)= |BP| : |PC|]=
1 : 2 ⇒ 2sinx= sin(60
o−x) ⇔
⇔ sinx= sin60
ocosx− cos60
osinx ⇔ 2sinx=
12√3cosx−
12sinx /*2 ⇔
⇔ 4sinx=
√3cosx− sinx ⇔ 5sinx=
√3cosx /:5cosx ⇔
tgx= 15√3. ...

27 gru 15:58
Eta:

|AD|=DC|=|AC|=4 trójkąt ADC jest równoboczny( wykaż samodzielnie)
to|DK|=|KC|=2| i ∡BDK|=120
o
|BK|= x wyznacz z tw. kosinusów w trójkącie BDK
otrzymasz Odp: |BK|= 2
√7 [j]
27 gru 16:38
Eta:
Zapomniałam dopisać,że to
zad.2 
27 gru 16:40
agent0013: Eta: jak wykazać, że to jest trójkąt równoboczny?
próbowałem z cechy trójkątów przystających, ale coś nie wyszło ;<
27 gru 18:28
Eta:
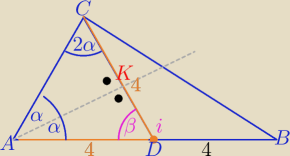
Najpierw zauważasz, że trójkąt ADC jest równoramienny, o ramionach
4
to |∡DAC|=|∡ACD|=2α i AK jest dwusieczną prostopadłą dośrodkowej CD
stąd w trójkącie prostokątnym ACK : α+2α=90
o ⇒ α= 30
o
W trójkącie prostokątnym ADK α+β= 90
o ⇒ β= 60
o= 2α
zatem trójkąt ADC jest trójkątem równobocznym o boku |AC|=|AD|=CD|=4
to |DK|=2 i |∡BDC|=120
o
i dalej już tak jak napisałam ............
Pozdrawiam

27 gru 20:49
agent0013: dzieki ; )
27 gru 22:53
agent0013: to zostało jeszcze zadanie 3. może ktoś ma jakiś pomysł?
27 gru 23:59
Eta:
Poproś ładnie
Milę , bo niedawno to zadanie rozwiązywała

28 gru 00:04
Mila:
Jutro, bo sporo rysowania i pisania .
Dobranoc

28 gru 00:30
pigor: ..., niech r=?. to z warunków zadania zad.3a. np. tak :
AD2=(20−r)(20+r) i AD+rAD= 3520 ⇔ AD2=202−r2 i 20AD+20r=35AD ⇔
⇔ AD2=202−r2 i 4r=3AD ⇒ 16r2=9(202−r2) ⇔ 25r2=602 ⇒ 5r=60 ⇔ r=12.
28 gru 00:33
pigor: ..., no to
3b. np. tak:
r=12 i
PB=x=?, a
PE=y=?,
| | y | | 12√2 | |
to np. |
| = |
| i y(y+12√2)= (x+15−12)(x+15+12) ⇒ |
| | x | | 15 | |
⇒ (*)
y= 45√2x i y
2+12
√2y= (x+3)(x+27) ⇒
⇒
3225 x
2+
965 x= x
2+30x+81 /*25 ⇔ 32x
2+5*96x−25x
2−750x−81*25=0 ⇔
⇔
7x2−270x−81*25=0 i Δ= 270
2+7*81*100= 72900+56700= 360
2 ⇒
⇒
x= 114(270+360)=
45 >0, stąd i z (*)
y=45√2*45=
36√2.

28 gru 01:21
Eta:
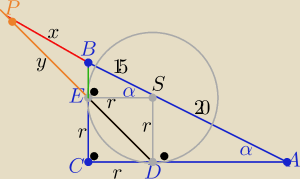
| | 20 | | 4 | |
a)Z podobieństwa trójkątów ADS i EBS z cechy (kkk) w skali k= |
| = |
| |
| | 15 | | 3 | |
| | 4 | | 3 | |
|DA|= |
| r i |EB|= |
| r , r>0 |
| | 3 | | 4 | |
| | 16 | |
z tw. Pitagorasa w ΔADS: r2+ |
| r2=400 ⇒ 25r2=9*400 to r2=144 ⇒ r=12 |
| | 9 | |
Z podobieństwa trójkątów DSP i EBP: z cechy (kkk)
| |DS| | | x+15 | | 12 | | 4 | | x+15 | |
| = |
| ⇒ |
| = |
| = |
| |
| |EB| | | x | | 9 | | 3 | | x | |
| | y | | |ED| | | y | | 12√2 | |
to |
| = |
| ⇒ |
| = |
| ⇒ y= 36√2 |
| | x | | 15 | | 45 | | 15 | |
Myślę ,że mniej "zamulone" jest moje rozwiązanie

28 gru 03:11
agent0013: bardzo dziękuję za pomoc

28 gru 11:49
Mila:
Nocne Marki.
Cóż , to miło, że już rozwiązane , narysowane, zapisane.

dla
Ety i pigora
28 gru 18:51
Eta:

28 gru 18:55

 |AD|=DC|=|AC|=4 trójkąt ADC jest równoboczny( wykaż samodzielnie)
to|DK|=|KC|=2| i ∡BDK|=120o
|BK|= x wyznacz z tw. kosinusów w trójkącie BDK
otrzymasz Odp: |BK|= 2√7 [j]
|AD|=DC|=|AC|=4 trójkąt ADC jest równoboczny( wykaż samodzielnie)
to|DK|=|KC|=2| i ∡BDK|=120o
|BK|= x wyznacz z tw. kosinusów w trójkącie BDK
otrzymasz Odp: |BK|= 2√7 [j]

 Najpierw zauważasz, że trójkąt ADC jest równoramienny, o ramionach 4
to |∡DAC|=|∡ACD|=2α i AK jest dwusieczną prostopadłą dośrodkowej CD
stąd w trójkącie prostokątnym ACK : α+2α=90o ⇒ α= 30o
W trójkącie prostokątnym ADK α+β= 90o ⇒ β= 60o= 2α
zatem trójkąt ADC jest trójkątem równobocznym o boku |AC|=|AD|=CD|=4
to |DK|=2 i |∡BDC|=120o
i dalej już tak jak napisałam ............
Pozdrawiam
Najpierw zauważasz, że trójkąt ADC jest równoramienny, o ramionach 4
to |∡DAC|=|∡ACD|=2α i AK jest dwusieczną prostopadłą dośrodkowej CD
stąd w trójkącie prostokątnym ACK : α+2α=90o ⇒ α= 30o
W trójkącie prostokątnym ADK α+β= 90o ⇒ β= 60o= 2α
zatem trójkąt ADC jest trójkątem równobocznym o boku |AC|=|AD|=CD|=4
to |DK|=2 i |∡BDC|=120o
i dalej już tak jak napisałam ............
Pozdrawiam 






 dla Ety i pigora
dla Ety i pigora
