Planimetria
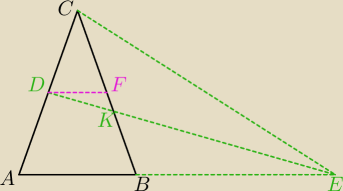
agent0013: 1. W trójkącie równoramiennym ABC: |AC|= |BC| i punkt D jest środkiem boku AC. Na przedłużeniu
boku AB wybrano punkt E. Oznaczmy |BE|= n*|AB|, n>0 (patrz rysunek). Udowodnij,
że punkt przecięcia odcinka DE z ramieniem BC dzieli to ramię w stosunku (n+1)/n
rysunek:
http://i60.tinypic.com/1eq72o.jpg
2. W trójkącie równoramiennym ABC, w którym |AB|=6 i |AC|=|BC|=9 poprowadzono wysokości AK i
BM. Oblicz długość odcinka KM.
26 gru 20:22
===:
| n*|AB| | | |BK| | |
| = |
| |
| 0,5*|AB| | | |FK| | |
| | |BK| | |
2n= |
| |BK|=2n*|FK| |
| | |FK| | |
|CK|=|BK|+2|FK|
| |BK|+2|FK| | | 2n*|FK|+2|FK| | | 2n+2 | | n+1 | |
| = |
| = |
| = |
| |
| |BK| | | 2n*|FK| | | 2n | | n | |
26 gru 21:53
Eta:
Za bardzo "na sucho" ( zabrakło
π... 
Brak dokładnych objaśnień , komentarzy .....
26 gru 22:17
Eta:
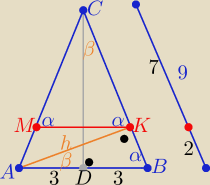
Z tw.Pitagorasa w ΔDBC
h=
√81−9=6
√2
| | h*9 | |
P(ΔABC)=18√2 to |
| =18√2 ⇒ h= 4√2 |
| | 2 | |
z tw. Pitagorasa w ΔABK
|BK|=
√36−32= 2 , to |CK|=7
Trójkąty ABC i MKC są podobne z cechy (kkk)
| | |AB| | | 9 | | 7 | | 14 | |
stąd: |
| = |
| ⇒ |MK|= |
| *6= |
| |
| | |MK| | | 7 | | 9 | | 3 | |
26 gru 22:29
Eta:
A
agent0013 świętuje
26 gru 22:31
===:
...
πigwówki Ci u nas dostatek −
26 gru 22:33
Eta:
Hehe .... u mnie też , bo sił brakuje
26 gru 22:34
agent0013: dzieki dzieki ^^
no tak . święta są to trzeba świętować i jeść . xD
jak Wam tak dobrze idzie .. to mam jeszcze jedno zadanie :
3. W trójkącie o obwodzie 20 jeden z boków ma długość 7, a przeciwległy mu kąt ma miarę 60.
oblicz pole tego trójkąta
27 gru 12:30
agent0013: * już nieaktualne
udało mi sie to rozwiazac ; >
27 gru 14:49
