funkcja kwadrat. abc: Funkcja kwadratowa f(x) = ax2 + bx − 3 ma różne miejsca zerowe, z których jedno jest równe − 3. Wiedząc, że funkcja ta przyjmuje najmniejszą wartość − 4, oblicz współczynniki a i b i narysuj wykres funkcji g(x) = − f(x + 1) − 2.

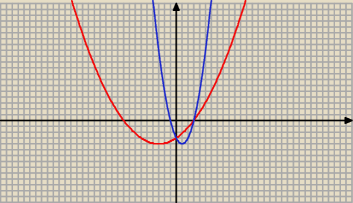
Janek191: f(x) = a x² + b x − 3 f( 3) = 0 więc a*9 + b*3 − 3 = 0 9 a + 3 b − 3 = 0 / : 3 3 a + b − 1 = 0 ⇒ b = 1 − 3a czyli f(x) = a x² + ( 1 − 3 a) x − 3 oraz q = − 4 i a > 0 Δ = ( 1 − 3 a)² − 4 a*(−3) = 1 − 6 a + 9 a² + 12 a = 9 a² + 6 a + 1 = ( 3 a + 1)²

	− Δ		− 9 a2 − 6 a − 1
q =		=		= − 4
	4 a		4a

− 9 a² − 6 a − 1 = − 16 a − 9 a² + 10 a − 1 = 0 9 a² − 10 a + 1 = 0 Δ₁ = 100 − 4*9*1 = 64 √Δ₁ = 8

	10 − 8		1		10 + 8
a =		=		lub a =		= 1
	18		9		18

więc

	1		2
b = 1 −		=		lub b = 1 − 3 = − 2
	3		3

Mamy

	1		2
f(x) =		x2 +		x − 3 lub f(x) = x2 − 2 x − 3
	9		3

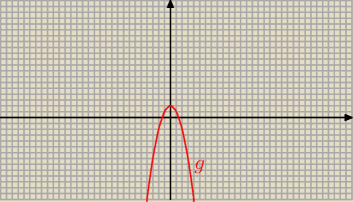Janek191: cd. g(x) = − f( x + 1) − 2 dla f(x) = x² − 2 x − 3 g(x) = − ( (x + 1)² − 2*( x + 1) − 3) − 2 = − ( x² + 2 x + 1 − 2 x − 2 − 3 ) − 2 = = − ( x² − 4) − 2 = − x² + 2