Pole części wspólnej 4 kół.
xcc: Środki czterech kół o promieniu a znajdują się w wierzchołkach kwadratu o boku a. Znajdź pole
części wspólnej danych czterech kół.
Powiem szczerze, że siedzę nad tym zadaniem ponad godzinę i nadal nie potrafię go zrobić. Macie
jakieś pomysły?
25 gru 21:00
utem:
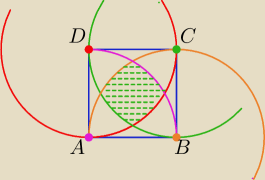
25 gru 21:10
:): a masz wynik?
bo ta rozeta w środku kwadratu, to 2 półkola o srednicy a√2 chyba
25 gru 21:12
utem:
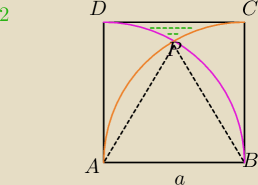
| | 1 | |
PΔDPC=a2−[PΔABP+ |
| πa2]− pole Δ "krzywoliniowego zielonego" |
| | 6 | |
| | a2√3 | | 1 | | a2√3 | | 1 | |
PΔDPC=a2−[ |
| + |
| πa2]=a2− |
| − |
| πa2 |
| | 4 | | 6 | | 4 | | 6 | |
| | 1 | |
PΔDBC= a2− |
| πa2 −pole Δ "krzywoliniowego dużego" |
| | 4 | |
cdn
25 gru 21:37
xcc: Nie, niestety nie mam odpowiedzi, bo dostaliśmy tylko kserówki z tego. Utem, dziękuję Ci
bardzo, nie wpadłbym chyba na to jak to obliczyć, bo teraz gdy mamy pole tej figury to mamy
już chyba praktycznie wszystko. Jeszcze raz dzięki i życze wesołych Świąt!

25 gru 21:45
utem:
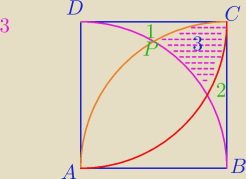
P
płatka3=P
ΔDBC−2*P
ΔDPC=
| | 1 | | a2√3 | | 1 | |
=a2− |
| πa2−2*[a2− |
| − |
| πa2]= |
| | 4 | | 4 | | 6 | |
cdn
25 gru 21:45
utem:
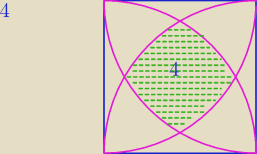 ======================
======================
Wesołych świąt.
25 gru 21:49



 Ppłatka3=PΔDBC−2*PΔDPC=
Ppłatka3=PΔDBC−2*PΔDPC=
