Funkcja Dżepetto 18:

	2x + a
Do wykresu funkcji opisanej wzorem f(x) =		należy punkt A = ( −1, 1 ).
	x − b

Wiedząc, ze dziedziną funkcji jest zbiór R \ { −2 } , wyznacz zbiór wartości funkcji i jej miejsca zerowe.

:):

	−2+a
1=
	−1−b

	2x+a
0=
	x−b

Dżepetto 18: Niestety nie rozumiem co dało nam podstawienie do funkcji pkt A. Co do drugiej linijki szukając miejsc zerowych też dalej nie mam pojęcia co z tym zrobić i co z tym a i b.

:): z 1 wyszło a+b=1, myslę

:):

	a
z 2 wyszło x0= −
	2

Dżepetto 18: Racja, z jedynki wyszło a+b=1 choć nie rozumiem 2. gdzie zniknęło b; jak wyliczyłeś miejsce zerowe x₀ oraz co z tym ZW?

:): ułamek jest równy 0, jesli mianownik jest równy 0 , x≠b

Dżepetto 18: Oczywiście Lecz masz może jakiś pomysł jak ZW tej funkcji?

	a
Jedno polecenie zrealizowane i zrozumiane mz = −
	2

:): no to mamy tak a+b=1 i U4−a}{2+b}∊ZW

	2x+a		4−a
ZW={		; x≠ −2 i a+b=1} \ {		}
	x−b		2+b

:):

	4−a
*		∉ZW
	2+b

Dżepetto 18:

	a
Zatem ostateczna odpowiedź to x0= −		a ZW zawiera się w 2 "wyrażeniach"?
	2

	2x+a
Pierwsza z nich		−warunek do niej to x≠ −2 a druga: a+b=1 i załozeniem do niej
	x−b

	4 −a
jest		? czy coś pomyliłem
	2+b

:): nie, ZW to ten zbiór co napisałam, a i b to parametry, od nich zależy wartość funkcji, dla konkretnych argumentów

:): 4−a/2+b to wyłączona wartość dla x=−2, który nie należy do dziedziny

Dżepetto 18: Właśnie nie wiem jak interpretować zapis ZW ZW={2x+a/x−b , x≠2, a+b=1} \ f(−2) czy może ZW={2x+a/x−b} \ f(−2) i założenia obok : x≠2 ⋀ a+b=1?

:): ZW to zbiór, a założenia na elementy należy umieszczac w zapisie zbioru co jest nie tak z moim zapisem? z 16,56? 4−a/2+b to liczba, która nie jest wartością

Dżepetto 18: Czyli pisząc na kartce mam zapisać ZW dokładnie tak jak zapisałeś go w 16:56 czy może mam napisać recznie jakiś inny znak zamiast ";"? Niestety z załozeniami na elementy spotykam sie chyba pierwszy raz =p

:): dokładnie tak jak napisałam

Dżepetto 18: Merci beaucoup!

megi:

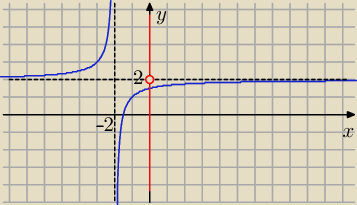
	2x+a		−2+a
f(x)=		⇒ f(−1)=		= −2+a
	x+2		−1+2

f(−1)=1 ⇒ a−2=1 ⇒ a= 3

	2x+3		2(x+2)−1		−1
f(x)=		=		= 2+		, u[−2,2]
	x+2		x+2		x+2

ZW=R \ {2}

megi: Jeszcze miejsce zerowe f(x):

	3
f(x)=0 ⇔ 2x+3=0 ⇒ xo=−
	2

Dżepetto 18: Teraz widzę wszystko jak na dłoni. Megi po x kolejny ratujesz, dzięki

Dżepetto 18: Choć mam jedno pytanie; skąd wzięło się +2 w mianowniku zamiast −b?

megi:

	2x+a
Z dziedziny : D= R\{−2} ⇒ b= −2 to f(x)=
	x+2

:): ale b to parametr, argument to x ? to x≠ −2

megi:

	2x+a
Jeżeli D=R\ {−2} to f(x)=		⇒ b= −2
	x+2

megi: @ : ........... za dużo "napoju" było?

:): dalej nie rozumiem, "napojów" nie było, ale wierze na słowo, ja dawno to "brałam"

megi:

	3
Odgadnij "b" jeżeli D= R\{1} dla f(x)=
	x+b

:): b= −1?

megi: No i ok

megi: I podobnie w tym zadaniu podanym przez Dżepetto18

:): teraz kapuje jestem mądrzejsza troszkę znowu nie zajarzyłam wczesniej dzięki

Dżepetto 18: Oczywiście, megi dziękuję za wyjaśnienie PS. Polecam hobbit bitwa 5−ciu armii; wczoraj nie odp bo zapadła szybka decyzja żeby na niego skoczyć