Funkcja Dżepetto 18: Dana jest funkcja kwadratowa f(x) = (m − 1)x² + (2m + 4)x − 6. Funkcja g(m) przyporządkowuje każdej liczbie rzeczywistej m liczbę różnych miejsc zerowych funkcji f(x). Podaj wzór i narysuj wykres funkcji g(x)

:): Δ=(2m+4)²+24(m−1)=?... >0 trzeba ustalic dziedzinę tej funkcji ↓ g(x)

Dżepetto 18: Dziedzina już jest: Δ_m = 6√3 i m₁=−5−3√3 oraz m₂=−5+3√3 m∊ (−∞, −5−3√3) suma (−5+3√3, +∞) nadal nie wiem co z g(x) :c

megi: Wskazówka 0 −− miejsc zerowych dla m≠1 ⋀ Δ<0 1 −− miejsce zerowe dla m=1 lub m≠1 ⋀ Δ=0 2 −−− miejsca zerowe dla m≠1 ⋀ Δ>0 {0 dla m .......... g(m)={1 dla m .......... {2 dla m........

Dżepetto 18: megi, niestety nadal nie wiem jak ruszyć, g(m) przyporządkowuje każdej liczbie R m liczbę róznych ms_z funkcji f(x) :c

:): g(m) przyjmuje wartości {0,1,2} w zależności od m więc masz wzór powyżej

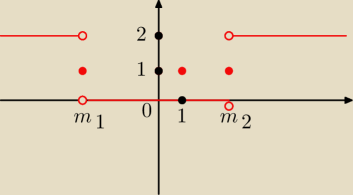
:): m₁ i m₂ to m₀ Δ

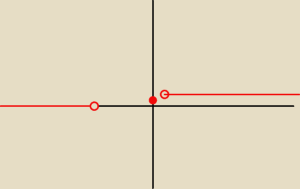
Dżepetto 18: Zatem {0 dla m∊(−∞, −5−3√3) g(m)= {1 dla m=1 {2 dla m∊(−5+3√3,+∞) Dobrze zrozumiałem?

Dżepetto 18: Oczywiście, Twój wykres jest dobry

:): nie uwzględniłes znaku Δ dla m

Dżepetto 18: { 0 dla m∊ (m₁,m₂ g(m) { 1 dla m∊{m₁,1,m₂ { 2 dla m∊(−∞,m₁) suma (m₂, +∞)

Dżepetto 18: *(m₁,m₂) {M₁,1,m₂}

:):

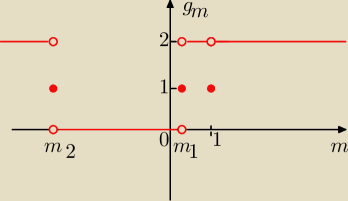
megi: Nie chciało się obliczać? 1 −− miejsce zerowe: gdy m=1 ⇒ f(x)=6x−6 −−f. liniowa , x_o=1 gdy m≠1 i Δ=0 to (2m+4)²+24(m−1) =0 ⇒ m²+10m−2=0 ⇒ m= −5+3√3 v m= −5−3√3 0 −− miejsc zerowych gdy m≠1 i Δ<0 to m∊( −5−3√3, −5+3√3) 2 −− miejsca zerowe gdy m≠1 i Δ>0 to m∊[(−∞, −5−3√3) U(−5+3√3,∞)] \{1} Teraz zapisz g(m) tak jak podałam i wykres ........

megi:

:): 0, m≠1i m∊m₁,m₂ 1, m=1 lub m≠1 i m={m₁,m₂} 2, m≠1i m∊(−∞m₁)∪(m₂,∞) chyba lepiej tak

:): no fakt megi, nie wzięłam pod uwagę, że moje m₂ <1 sorki

Dżepetto 18: Ok megi i wszystko zrozumiałem, wielkie dzięki! Ps. Megi dziękuję za przybliżenia