| x−2 | ||
log2 | ≥ 4x−x2 | |
| 2 |
| x−2 | ||
Niech f(x) = log2 | − 4x+x2. | |
| 2 |
| 1 | 1−4x+8+2x2−4x | 2x2 −8x +9 | 2(x−2)2+1 | |||||
f'(x) = | − 4+2x = | = | = | >0 | ||||
| x−2 | x−2 | x−2 | x−2 |
| x−2 | ||
a) x≥4 ⇒ f(x)≥f(4)=0 czyli dla x≥4: log2 | ≥ 4x−x2 − OK | |
| 2 |
| x−2 | ||
b) x<4 ⇒ f(x)<f(4)=0 czyli dla x<4: log2 | < 4x−x2 − źle | |
| 2 |
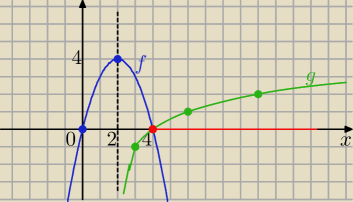 Wystarczy narysować wykresy:
f(x)= log2(x−2)−1 , x>2 krzywa logarytmiczna y= log2x po translacji o wektor
[2,−1]
g(x)= −x2+4x −−− parabola
Obydwa wykresy przecinają się w punkcie (4,0)
g(x)≥f(x) ( wykres g(x) nad wykresem f(x) dla x≥4
i to wszystko
Wystarczy narysować wykresy:
f(x)= log2(x−2)−1 , x>2 krzywa logarytmiczna y= log2x po translacji o wektor
[2,−1]
g(x)= −x2+4x −−− parabola
Obydwa wykresy przecinają się w punkcie (4,0)
g(x)≥f(x) ( wykres g(x) nad wykresem f(x) dla x≥4
i to wszystko
 poprawiam chochlika ...w oznaczeniach kolorów funkcji
ma być:
g(x)= log2(x−2)−1
f(x)= −x2+4x
poprawiam chochlika ...w oznaczeniach kolorów funkcji
ma być:
g(x)= log2(x−2)−1
f(x)= −x2+4x

 z jakiej okazji?
z jakiej okazji?
