Wyznacz równanie okręgu.
Adam: Prosta 2x−y−5=0 przecina okrąg o środku S(2,4) w punktach A i B. Długość cięciwy AB wynosi
4√5. Wyznacz równanie tego okręgu.
Wyznaczyłem równanie (x−2)2 + (y−4)2=r2. Pozostało mi wyznaczyć r. Jak to zrobić?
23 gru 21:59
Tadeusz:
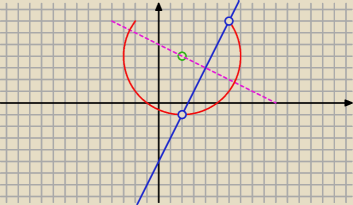
23 gru 22:26
Tadeusz:
... napisz przez S prostą prostopadłą do dane prostej.
Wyznacz punkt przecięcia będący środkiem cięciwy.
Potem współrzędne A i promień
23 gru 22:29
pigor: ..., lub niech S' rzut prostokątny środka S okręgu na dana prostą, to ,
| | |2*2−4−5| | | |−5| | |
|SS'|= |
| = |
| = √5, więc z tw. Pitagorasa |
| | √4+1 | | √5 | |
dla np.ΔAS'S:
SA2= SS' 2+AS' 2 ⇒ r
2=
√52+(2
√5)
2 ⇒
⇒ r
2= 5+4*5 ⇒
r2= 25 , zatem
(x−2)2+(y−4)2= 25 − szukane równanie.

23 gru 23:47
Adam: Narysowanie tej cięciwy rozumiem, wszystko ok bo mamy podane równanie prostej to wiemy jak
narysować, ale prosta prostopadła do tej cięciwy narysowana na ''oko'' jest chyba
niewystarczająca. Myślę że to trzeba udowodnić jakoś tylko nie wiem jak bo na oko można wtedy
zadania nie zaliczyć tak mi się zdaje. Poza tym jak mam wyznaczyć współrzędne A i B ? A
jeszcze poza tym to skąd mam wiedzieć że punkty A i B znajdują się właśnie w tym punkcie co
narysowałeś? Mogą przecież się znajdować ''kratkę'' dalej? Wytłumaczysz i pomożesz?

Sorki
że w święta i nie oczekuję szybkiej odpowiedzi

25 gru 19:16
===:
.. to nie jest prosta prostopadła narysowana na oko ...
To jest prostopadła do danej prostej a jednocześnie przechodząca przez punkt S

!
Punkt jej przecięcia z AB wyznacza środek tego odcinka (dlaczego

?)
Dalej to już banał −

25 gru 19:21
Adam: Ok niech będzie

Ogólnie to ja widzę że jest to prostopadła i wiedział bym jak ją narysować
tylko w książce w odpowiedziach znalazłem że 1 etap rozwiązania zadania to wyznaczenie
równania prostej prostopadłej do cięciwy AB także się zdziwiłem i nie wiedział bym jak napisać
to równanie. A poza tym dalej twierdzę, że te współrzędne punktów A i B nie muszą leżeć w
miejscu w którym kolega narysował. Mogą leżeć np. kratkę dalej w taki sposób, że nadal punkt S
będzie środkiem okręgu. Nie wiem, chyba że majaczę

25 gru 19:31
===:
Świątecznie "majaczysz"
To gdzie leżą punkty A i B (czyli ich współrzędne) to wyliczysz ... jeśli będziesz chciał −

Póki co to wiemy , że należą one zarówno do cięciwy jak i okręgu.
A Ciebie pytają o promień okręgu to o jest niezbędny do napisania równania −

25 gru 20:18


 Sorki
że w święta i nie oczekuję szybkiej odpowiedzi
Sorki
że w święta i nie oczekuję szybkiej odpowiedzi 
 !
Punkt jej przecięcia z AB wyznacza środek tego odcinka (dlaczego
!
Punkt jej przecięcia z AB wyznacza środek tego odcinka (dlaczego  ?)
Dalej to już banał −
?)
Dalej to już banał −
 Ogólnie to ja widzę że jest to prostopadła i wiedział bym jak ją narysować
tylko w książce w odpowiedziach znalazłem że 1 etap rozwiązania zadania to wyznaczenie
równania prostej prostopadłej do cięciwy AB także się zdziwiłem i nie wiedział bym jak napisać
to równanie. A poza tym dalej twierdzę, że te współrzędne punktów A i B nie muszą leżeć w
miejscu w którym kolega narysował. Mogą leżeć np. kratkę dalej w taki sposób, że nadal punkt S
będzie środkiem okręgu. Nie wiem, chyba że majaczę
Ogólnie to ja widzę że jest to prostopadła i wiedział bym jak ją narysować
tylko w książce w odpowiedziach znalazłem że 1 etap rozwiązania zadania to wyznaczenie
równania prostej prostopadłej do cięciwy AB także się zdziwiłem i nie wiedział bym jak napisać
to równanie. A poza tym dalej twierdzę, że te współrzędne punktów A i B nie muszą leżeć w
miejscu w którym kolega narysował. Mogą leżeć np. kratkę dalej w taki sposób, że nadal punkt S
będzie środkiem okręgu. Nie wiem, chyba że majaczę 
 Póki co to wiemy , że należą one zarówno do cięciwy jak i okręgu.
A Ciebie pytają o promień okręgu to o jest niezbędny do napisania równania −
Póki co to wiemy , że należą one zarówno do cięciwy jak i okręgu.
A Ciebie pytają o promień okręgu to o jest niezbędny do napisania równania −