geometria na płaszczyźnie kartezjańskiej Maturalna 96': Z serii: geometria na płaszczyźnie kartezjańskiej na święta. Zinterpretuj algebraicznie obszar ograniczony krzywą y + | x − 1 | − 2 = 0 i okręgiem przechodzącym przez punkty A = ( −3, −2), B = ( 1 + 2√7, 0), C = ( 5, 6) oraz oblicz pole tego obszaru

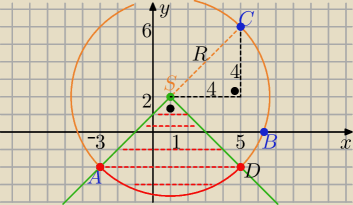
megi: A(−3,−2), C(5,6) , B(1+2√7,0) S(x,y) i R²=|AS|²=|CS|²=|BS|² zatem: (x+3)²+(y+2)²=(x−5)²+(y−6)² ⇒ ........... x+y=3 ⇒ y= 3−x i |BS|²=|AS|² ⇒ .............. −4x(1+√7)= −4(1+√7) ⇒ x=1 i y=2 S(1,2) i R²= ...........=32 y= −|x−1|+2 i S∊ (y= −|x−1|+2) i D(5, −2) Proste AS i DS są prostopadłe , bo a_AS=1 i a_SD= −1

	1
Pole szukanego obszaru, to pole wycinka ADS=		P(koła)
	4

	1
Pw=		πR2= ..... = 8π[j2]
	4

Wesołych Świąt

5-latek: megi Wesołych Świąt

Kacper: Dlaczego megi?

Eta: