równania wielomianowe iksa: Zapisać zbiór rozwiązań podanej nierówności w postaci przedziału. (|x|−1)²⁰¹³ * (|x|−2)²⁰¹⁴) > 0 Jak to zrobić, gdy jest wartość bezwzględna ?

:): IxI=x, x>0 IxI=−x, x<0

iksa: ale to i tak nie wiem, bo gdy byłoby bez wartości bezwzględnej to zaznaczam miejsca zerowe i rysuję a w takim przypadku ?

:): rozpatrujesz 2 przypadki i sumujesz przedziały

iksa: czyli będzie x∊ (−1;1) u (1;2) u (2;∞) ?

gwiazdka:

:): możez jeszcze zrobic to prościej

:): iloczyn jest dodatni, jesli oba czynniki maja ten sam znak

iksa: aaaa super, dzięki wielkie !

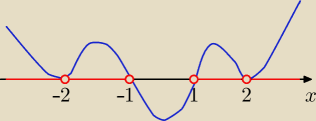
gwiazdka: |x|−1=0 ⇒ x= −1 v x=1 |x|−2=0 ⇒ x= −2 v x= 2 teraz uwzględnij krotność pierwiastków ( jak na rys.)

pigor: ..., zapisać zbiór rozwiązań podanej nierówności (|x|−1)²⁰¹³ * (|x|−2)²⁰¹⁴ >0 w postaci przedziału. −−−−−−−−−−−−−−−−−−−−−−−−− czyli możemy to zapisać np. tak : (|x|−1)²⁰¹³ * (|x|−2)²⁰¹⁴ >0 ⇔ (|x|−1 >0 i |x|−2≠0) ⇔ ⇔ (|x| >1 i |x|≠2) ⇔ (x< −1 v x>1) i x∊R\{−2,2} ⇔ ⇔ x∊(−∞;−2) U (−2;−1) U (1;2) U (2;+∞) . ...