zadanko
Blue: W ostrosłupie prawidłowym czworokątnym wysokość jest równa h i tworzy z krawędzią boczną kąt
45
0. Ostrosłup ten przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do
podstawy pod kątem 60
0. Oblicz pole otrzymanego przekroju.
Problemem jest obliczenie wysokości przekroju, wiem, że podstawa będzie 2h, ale co z tą
wysokością
Czy tam będą jakieś trójkąty podobne?
22 gru 16:17
J:
wysokość przekroju tworzy z połową przekątnej podstawy kąt 60 − stąd wysokość przekroju
pole przekroju to połowa iloczynu przekatnej podstawy i wysokości przekroju ...
22 gru 16:27
J:
..pospieszyłem się, nie było wpisu ...
22 gru 16:31
Blue: No właśnie coś mi się nie zgadza, bo skąd wiesz, że z połową przekątnej
22 gru 16:36
kyrtap: Blue zastosuj tw. sinusów
22 gru 16:37
kyrtap:
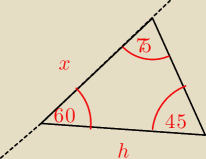
będziesz miała tam taki trójkąt
22 gru 16:40
J:
..to na pewno, bo podstawa przekroju to przekątna podstawy bryły ...
22 gru 16:41
kyrtap: przy okazji będziesz musiała zastosować wzór sin(α+ β)
22 gru 16:42
J:
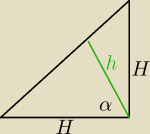
α = 60
o
H = wysokość bryły
h − wysokość przekroju
22 gru 16:45
kyrtap: Blue sobie poszła
22 gru 17:09
Blue: Już jestem
22 gru 17:12
kyrtap: No i jak sprawa wygląda u Ciebie z tym przekrojem?
22 gru 17:14
Blue: Dzięki kyrtap
22 gru 17:14
Blue: Wygląda tak, że zaraz zacznę liczyć z tego tw.sinusów
22 gru 17:15
Blue: Wyszło dobrze
P= h
2(
√3−1)
22 gru 17:20
kyrtap: czasami coś mądrego wymyślę ale to się zdarza niestety rzadko
22 gru 17:21