styczna Kasia: Witam wszystkich, mam znalezc rownanie lini ktora bedzie styczna(tangent, nie wiem czy dobrze przetlumaczylam) do y=2^3x−1 w punkcie (1,4). Nie mam pojecia jak sie za to zabrac, nie bylo mnie wtedy na zajeciach na uczelni − a na internecie nie potrafie znalezc podobnego zadania. Prosze o jakies wskazowki, albo podobne zadanie, azebym mogla anaologicznie go zrobic. Z gory bardzo dziekuje za pomoc

jakubs: https://matematykaszkolna.pl/strona/379.html

Radek: Równanie stycznej y−y₀=f'(x₀)(x−x₀)

Kasia: y= 2^3x−1 y'= 2^3x−1*ln2 * 3 f(1)=4 f'(1)=12ln y−4=12ln(x−(4−12ln) I przykro mi, ale nie wiem co teraz :<

J:

	8x
źle pochodna ... f(x) =		... i teraz licz pochodną ...
	2

razor: pochodna akurat dobrze jest

J: racja ...teraz to widzę ...

Kasia: :(

razor: y = f'(x₀)(x−x₀) + y₀ (x₀,y₀) = (1,4) y = f'(1)(x−1) + 4 = (2²*ln2*3)(x−1)+4 = 12ln2(x−1)+4 = 12ln2*x − 12ln2+4 to już jest wynik

J: y − 4 = 12ln2(x −1) .... szukana styczna..

Kasia: Bardzo dziękuję, mam jeszcze jedno pytanie. Mam skany od kolegi i mam teraz dylemat : W zagadnieniach piszę: Styczna/normalna linia. Co znaczy ta normalna linia?

razor: normalna − prostopadła do stycznej

J: normalna, to prosta prostopadła do stycznej w punkcie styczności..

J: ..w punkcie styczności ...

Kasia: Przepraszam, to wiecie możę gdzie znajdę przykładowe tkaie zadanie?

J: spróbuj na tym przykładzie ... napisz równanie normalnej do tej krzywej w punkci (1,4) ..

Kasia: Niestety nie wiem jak to zrobić . Poszukam na internecie przykładowe zadanie i spróbuję wtedy

Kasia: y=2x³ −x² +1 p=(1,2) y' = 6x² −2x f(1)=2 f'(1)=4 y−2=4(x−1) Równanie stycznej: y=4x−2, no i teraz próbóje tę prostopadłą znaleźć − jakiekolwiek porady?

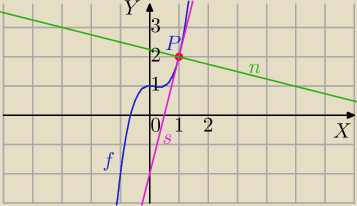
Mila: f(x)= 2x³ −x² +1, P=(1,2) a₁,a₂ wsp. kierunkowe dwóch prostych a₁*a₂=−1 to proste są prostopadłe s: y=4x−2

	1		1		9
n: y=−		x+b i (1,2) ∊prostej⇔2=−		+b, b=
	4		4		4

	1		9
n: y=−		x+
	4		4

Janek191: @Kasia Próbuję